Fox ＆ Mathematics 　　　　　〜べんきょう、しよう〜 　　関数のお話 「行ってらっしゃーい」 アパートのドアの前。大きく手を振る稲穂の姿。 「いってきまーす」 俺の隣から聞こえる、平和そうな声。 「留守番お願いねー」 「まっかしといてー」 いくら昼前とはいえ、少々近所迷惑じゃないだろうか。 そんなことを思いもしたが、案外すぐ稲穂は引っ込んだ。ちなみに前の巫女装束もどきではなく、普通の洋服だ。佐倉さんが貸してあげたらしい。 おかっぱ頭のヘアバンドは、相変わらず役不足っぽいが…… 「元気よね、稲穂ちゃんって」 「もう少し大人しくてもいいと思うんですけどね……」 昼から授業の俺。 昼から研究室へ行く佐倉さん。 まあ、たまにではあるが、こうして一緒に大学に行くこともある。 思い返せば、初めて話した同じ大学の人だったなあ。そう、あれは…… 「そういえば、昨日は分数やったのよね」 回想シーンに入ろうとしたところで、見事に邪魔されてしまった。 「え、なんですって？」 「だから、分数教えたんでしょう？　稲穂ちゃんに」 どうやら昨日のことを言っているらしい。 「ああ、ええ。そうですよ……もっとも、あいつはすでに知ってたみたいですが」 義務教育を受けていなさそうな微妙な発言もあったが…… 「分数だもんね。お母さんに教えてもらったって言ってたわ」 「そんなことも言ってましたね……」 というか、そんなことは可能なのか？　法律は詳しくないからなんとも言えないが……義務を放棄しちゃだめだろう。 ふと、昨日佐倉さんが言っていたことを思い出した。 「そういえば、稲穂の秘密ってなんなんですか？」 「だから、秘密」 悪戯っぽく笑う佐倉さん。 「佐倉さん……」 何か秘密にされながら勉強教えるのもなあ…… 「じゃあヒント。初めて稲穂ちゃんが都君の部屋に上がったときのこと思い出してみて」 「初めて部屋に来たとき？」 ドアに張り付いて中をうかがってた……じゃなくて、部屋に上がったときか。勉強が嫌で神社から来たとか何とか…… 「…………」 わからん。秘密にするような部分は…… あ、もしかしてあの火を出した手品か？ 「じゃあ、またね」 「あ、佐倉さん」 学部の違う俺と佐倉さん。 門をくぐったところで早々にお別れだ。 静止の声も届かず、佐倉さんの後ろ姿は人ごみにまぎれてしまった。 「なんだ、まったく……」 結局、分からないままだ。 「今日の勉強は、関数だ」 俺の言葉を聞いて、不思議そうな顔をする稲穂。 「かんすー？」 「そうだ」 「関スー……」 人差し指を口に当て、何か考えているようだ。 そして、開口一番。 「関西スーパー」 「違う！」 関西スーパーって、どういう発想だよ…… 「関数というのはだな……なんて説明すりゃいいんだ？」 つ、つまりだな…… 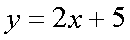こういうのは知ってるだろ？ これはつまり、xが決まればyも決まるよな。ｘ=4ならｙは１３だ。 そういう関係のことを、「ｙはｘの関数」と呼ぶわけだ。 で、一般的には、ｙのところを、ｆ(x)で表す。 つまりは、 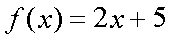というわけだ。 かっこに入っているｘは、これがｘの関数であることを示している。 ｘとｙの関数だったら、 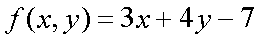とまあ、かっこの中にｘとｙの関数であることを示すわけだ。 え、なんでｆなのかって？ 関数っていうのは、英語でfunction（ファンクション）だから、その頭文字をとったんだ。 同じ問題で二つの関数が出てきた場合、次はなぜかｇで表すんだけどな。まあ、アルファベット順だろう。 でまあ、変数一つの関数の場合、グラフに書き出すのは簡単なんだ。 例をとってみると、 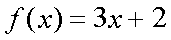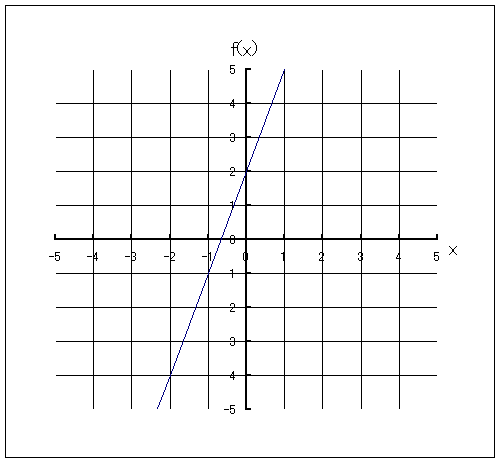こんな風に２次元になるからな。 グラフの書き方としては、ｘの各点をだな、０のとき、１のとき……というようにとっていけば一本の線になる。だが、１次関数の場合は傾きが一定だから、どこか一点……ま、ｘ＝０だな。それをとって、３の傾きでグラフを伸ばせばあっという間だ。 ああ、傾きってのは、ｘが１進んだときにｆ(x)がどれだけ増えるかってことな。 ちなみに変数二つだと3次元の立体グラフになってしまう。ｘとｙを決めると、答えはｚ方向の高さを表すからな。 変数が１次元ならグラフは２次元。変数が2次元ならグラフは3次元ってわけだ。 「ちょ、ちょっと待って……」 稲穂が頭を抱えていた。 「どうした？」 「１次関数と１次元って一緒なの？」 「ああ、それか……」 １次関数ってのは、変数が１次……つまり、 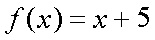こんなやつだ。 ちなみに２次関数ってのは、 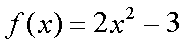こういう奴だ。 「ｘが２乗されてれば２次関数なの？」 お。2乗は知っていたか。 「まあ、そういうことだ」 じゃあこれはどうだ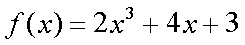？ 「え、えーっと……３次関数？」 「そうだ。つまり、ｘが最大何乗なのかってことだな。何次関数ってのは」 「そうなんだ……」 で、変数が１次元ってのは、 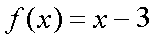対して２次元は、 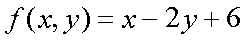まあ、一目瞭然だな。 変数が何種類あるかってことだ。 「ん、なんとなくわかった」 「なんとなくかよ……」 まあいいや。 じゃあ稲穂。ここで問題だ。 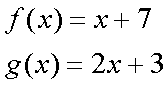この二つの関数がグラフ上で交わるｘはいくつだ？ 「え、えっと……ｘが０のとき……は違うし、１のときは……８と５だからダメ」 予想通り力技できたか……心の中で意地悪な笑み。 「ダメだな」 「ｘが２だったら、９と……７でダメ……４だと、１１と……１１？　あっ、分かった。４だ！」 当たりだ。じゃあ、これはどうだ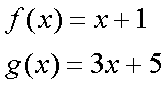？ 「え、えっと……０もだめ、１もだめ……ｘが２のときは３と１１で、ｘが３のときは４と……１４？　あ、あれ？」 ようやく気付いたらしい。 「どんどん離れていくんだけど……」 「そらそうだろう。答えは−2だからな」 「マイナスぅ？　達哉ずるい」 口を尖らせる稲穂。 可愛いというよりは面白い。 「ずるくない。そもそもそんな力技でやろうとするからダメなんだ」 いいか？ グラフ上で言えば、 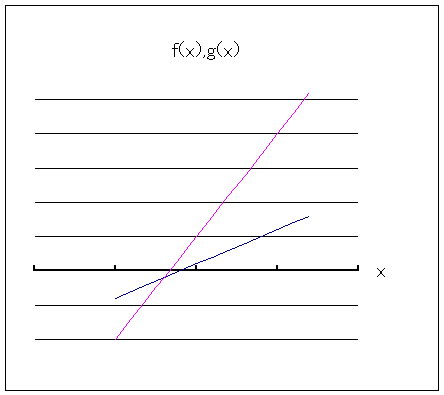こうなっている。この交わっている点なんだから、 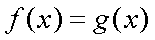つまりは、 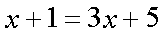ｘとそれ以外に移項してわけると、 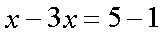計算すると、 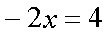ここで、直感的にｘは−２だとわかるんだが……詳しくやると、 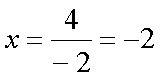ってわけだ。 「…………」 稲穂が固まっていた。 ちょっとペース速かったか……？ 「イコウって、何？」 そこからか！ 移項というのはだな……まあ、分数の割り算と理屈は似てるな。 全力で辻褄合わせてるんだ。 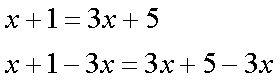同じ数を引いたら、まあ、その式は成り立ったまんまだよな。 これで右の３ｘが消えて、左の１を消すために、両辺から１を引く。 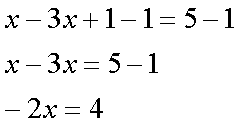「せこくない？」 「せこくない」 掛け算や分数の移項のときは、分数のときとほとんど同じだな。 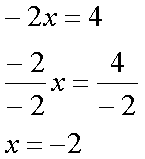ちなみに、 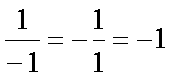だぞ。今更だが。 さっきの問題も、 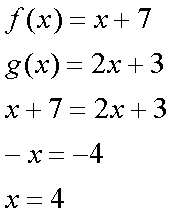ちなみに最後は両辺−1を掛けたことはわかるよな。 「ほんとだ。あっという間」 「ちなみに今日は1次関数ばかりやっているが、これははっきり言って中学生レベルだからな。程遠い」 「うー……」 何も言い返せない様子。やっと自分の力不足を思い知ったか。 「でもさ、達哉って物理の人なんでしょ？　リョウコも物理だよね？」 「リョウコ？　誰だそれ？」 「あれ。リョウコチカラガク」 量子力学か……またリキガク読めなくなってるし。 まあ、ハカルコからリョウコになっただけでも進歩か…… 「ねえ、物理なんでしょう？」 というか、他になんだって言うんだ。 「まあ、そうだが……」 そう答えると、稲穂は少し首をかしげた。 「じゃあなんで数学ばっかりやってんの？」 ああ、そういうことか……まあ、物理のぶの字も出てこなかったからな。 「物理ってのはな、自然界の法則や振る舞いを数式で表す学問なんだ。だから、道具として数学が必要なんだよ」 「ふーん……」 わかってねえな、こいつ…… よし、じゃあ次に教えることは…… 力学に行くために三角でも教えるかな。 とまあ、次のテーマも決まったところで、今日の勉強はお開きになったわけである。 戻る