力学初歩のお話

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　力学初歩のお話

授業が終わって帰り支度をしていると、
「……はぁ」
思わず出てくるため息。
「全く、意味がわからん……」
それはもちろん、昨日のことだ。

「な、なんなんだそれはっ！？」
風呂場にいる稲穂。その頭にある、狐の耳。
「えっと、都君、落ち着いて。ね？」
佐倉さんはちょっとおろおろ。
「そ、そうだよ達哉。ちょっと落ち着いてよ」
稲穂も少しあせっている。
「落ち着いていられるかっ！　な、なんなんだそれは！」
「……耳だけど」
ボソッとそう聞こえてきた。
「んなこたぁわかっとる！」
「ひゃっ」
と、声を上げたのは佐倉さん。
「……分かってるなら、聞かないでよ」
ちょっと不機嫌になる稲穂。
「そういう問題じゃなくてだな！」
「ちょっと、都君。あんまりうるさくすると誰か来ちゃうよ……？」
「そうだそうだー」
「くっ……」
た、確かに誰か来るとマズイ。女性の部屋に俺がいるってのもマズイ。何より稲穂の耳がばれて騒ぎになることがマズイ。
俺は押し黙らざるを得なかった。

「……落ち着いた？」
「なんとか」
佐倉さんが改めて入れなおしたお茶で、何とか話し合いが出来る状況になった。
だが、俺の間の前には相変わらず信じがたい稲穂の頭。
「で、それは一体なんなんだ？　というか、どういうことなのか説明してもらおうか」
「わかった……」
あっさりと稲穂はうなずいた。まあ、今更どうしようもないことは明白だが。
「佐倉さんも知ってましたね？」
「うん……」
すると、佐倉さんが言ってた稲穂の秘密ってのは、これだったのか……
お茶を一口すすると、稲穂が口を開いた。
「私が神社から来たって言ったのは覚えてるよね」
「ああ」
というか、その神社のまん前でぶつかったわけだしな。
「それでね、信じてもらえないかもしれないんだけど……私のお母さん、狐なの」
「はっ……？」
意味がわからなかった。狐？　はあ、狐……
頭についてんのは確かに狐の耳だろうが、うーん……
「話は長くなるから省略するんだけど……あ、お父さんは人間……ってお母さんは言ってた」
「お前は知らないのか？」
「うん……」
少し寂しそうな稲穂。
「はっ……」
なんというか、まあ、おかしな話ではあるよな。
おかしな話ではある。だが……
「信じない？」
「信じるも何も……」
稲穂の耳を引っ張ってみる。
「い、いたたた……やめてよ、達哉」
思ったより硬かった。これをヘアバンドでおさえていたんだから、かなりの苦労だ。
「火も出せただろ？」
初めて家に来た日のことを思い出しながら、稲穂に聞いた。
「え……うん。見る？」
「いや、いい」
まあなんというか、昔話に出てくる狐みたいなもんなんだろう。きっと。
「狐か……」
遺伝子の形がどうこうで不可能だとか聞いたこともあるが……まあ、目の前にある事実だけはどうしようもないしな。
じっと稲穂を見つめる。
見つめられた稲穂は、少し緊張しているように見える。追い出されるとでも思っているんだろうか。
「お前的にはどっちなんだ？」
「え？」
質問の意味がわからず、きょとんとする稲穂。
「狐なのか、人間なのか」
「うーん……人間、かな。狐としては半人前すぎるの……いろんな点で」
半人前ねえ。
「人間としても半人前じゃないか」
苦笑しながらそう言うと、
「あ、ひどーい」
少し表情がほぐれた。
「そうだよ、都君」
黙って見守っていた佐倉さんも苦笑する。
二人とも冗談だとわかってるようだ。
「それでね……お母さんは、そっちの勉強……あ、狐としてのね。そればっかりさせるから」
まあ、お母さんが狐ならそうだわな……というか、そのお母さんに家庭教師してもらったのか……？　最近の狐は中学生レベルの学力があるのか。
「自分が使えない、わかんない勉強しても、楽しくないでしょ？」
「それで、家出？」
佐倉さんが聞くと、
「うん……そうなる、かな」
目を伏せてうなずいた。
まあ、大体の事情はわかった。
いや、分からない部分は多々あるんだが……
「稲穂」
「うん？」
おかっぱの髪を揺らして、稲穂が顔を上げた。
「すぐじゃなくてもいいが、お母さんには言っとけ。ここで勉強してるって」
「うん……」
何も連絡してる様子はないからな。多少なりと心配してるだろう……
それともう一つ。俺は役不足ヘアバンドを手に取った。
「これ、苦しいんじゃないのか？」
「あ、うん……ちょっとね」
そりゃそうだろうな、これだけ立派な耳を押さえつけてたんだから。しかし、こんなヘアバンドごときで隠れてたとは、一種のミステリーでもある。
「じゃあ取っちまえ」
「え……」
ぴくっと稲穂の耳が動いた。
「勉強は、やりやすい環境でやるべきだ」
「あ……うんっ」
今日一番の嬉しそうな声だった。
まあ、乗りかかった船というか……仕方ないか。
多少情が移っているのも否定できない。
なんとなくそう思っていると、稲穂が立ち上がった。
「それとね、もう一つ……」

「よお、どうしたんだ？　ため息なんかついちまって」
教室を出たところで、米崎が話し掛けてきた。
「おう……まあ、悩める青年だからな」
冗談めかしたつもりだったが、あまり通じなかったようだ。
「意味が良くわからんが、まあがんばれや。そういや、カテキョの方はどうなのよ？」
「ああ、まあ、順調……かな」
勉強の方は。
「結構なことじゃないか」
けらけら笑う米崎。まあ、大まかな理解度は良いみたいだし、その点はいい。いいんだが……
「問題がないわけじゃない」
「へえ、好きにでもなっちまったか？」
笑いながらそんなことを聞いてきた。
「なんでそうなるんだよ……」
稲穂をねえ……
まあ、全くないとは言い切れないだろうが。あの性格は嫌いじゃないし。
しかし、好きとかそれ以前の問題だ。

「さて、物理をやるぞ」
「おおー……」
なにが『おおー』なのか分からないが、とりあえずやる気はあるようだ。
「まずは基本中の基本。力学だ」
「どんとこーい」
「ハイだな、お前……」
ちょっと引くぞ。
「自由に出していいんだもん、そりゃハイにもなるよ」
そう言ってぱたぱたと揺らす。尻尾を。
「さいですか……」
耳と尻尾……なんというか、意外と目のやり場に困った。

いきなりだが、根幹とも言える運動の三法則だ

慣性の法則
運動の法則
作用反作用の法則

「……覚えるの？」
ちょっと苦い顔をする稲穂。暗記は苦手なのかもしれない。
「覚えるんだ。まあ意味さえ覚えれば名前なんてどうでもいいし、そもそも名前なんて意味からつけられたものだから、意味がわかれば名前も分かる」
一つずつ説明していくことにした。
「慣性の法則ってのは、力がかからない物体は、ずっと同じ状態が続くってことだ。つまり、物は押さなきゃ動かない」
「うん、そうだよね」
これはまあ、イメージしやすいか。
「または、そのまま」
「そのまま？」
期待通り、その言葉に引っかかってくれた。
「スケートとかしたことあるか？」
なさそうだが。
「ない……けど知ってる」
「そうか……じゃあ、スケート場で人に押されたらどうなると思う？」
「氷の上でだよね……うーん、ずっと滑ってっちゃうかな」
正解。イメージする力はそこそこあるんだよな。
「まあ、そうだよな。実際は多少なりと摩擦があるからそうはいかないが。押されてそこからは止まらない」
しかし、説明しにくいな……
「地球の上じゃあ、どうしても重力があるから想像し辛いんだが、宇宙なんかではそうだよな。宇宙でボール投げたらどこまでも飛んでいく」
「あ、それは聞いたことあるよ」
稲穂の言動から判断するに、別にずっと神社にこもっていたってわけじゃないんだろう。
「んでまあそれは、次の運動の法則にも含まれている。運動の法則ってのは、運動方程式のことで、つまりこれだ」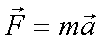

「Ｆとaはベクトルを表しているんだが……まあ今はそれを気にしなくてもいい」
「うん」
簡単な式をノートに書き写して、稲穂はうなずいた。
「Ｆは力。mは質量……まあ、重さだな。aは加速度を表している」
「なんで？」
「なんでって……何が？」
予期しないところで質問が出た。
「記号。日本語とかじゃダメなの？」
そうきたか……
「ＦはForce（フォース）、mはMass（マス）、aはAcceleration（アクセレーション）。全部英語から来てるの。もし日本語で表してみろ『ち＝しか』なんていう意味不明なものになっちまうぞ」
「それは変だね」
「だろ？」
分かってるなら聞くなよ……
「でまあ、力をかけた方向に、加速度が生じるってことだ。だから、力をかけなきゃ加速度は生じない。慣性の法則な」
「うんうん。当たり前だよね」
お。言い切ったな……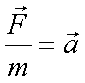

「この方が分かりやすいかな。力を質量で割ると、加速度が出る」
「何となく分かったよ。質量が大きいと、加速が鈍くなるんだよね？」
おお、えらく勘がいいじゃないか。
「そうだ。逆に力が大きいと、加速も大きくなる」
今感じているのが教師冥利という奴だろうか。ちょっとじーんと来たぞ。
と、こんな序盤でそんなこと言ってても仕方ないな。
「単位の話になるが、Fは[N]でニュートン。ｍは[kg]でキログラム。aは[m/s^2]でメートル毎秒毎秒とか、メートル毎セカンド二乗とかいろいろ言い方はある。ああ『^2』は二乗の意味な。単位のｍ（メートル）と式のｍ（質量）は別物だから注意するように」
ノートに書き取りながら、稲穂が苦い顔をする。
「うー、単位……？　キログラムとメートルしか知らないよ」
まあ、秒を『セカンド』とは言うまいよ……
「稲穂の体重は？」
「私はよんじゅう……って、何言わせるの！」
怒った。稲穂もやはり女の子ということか。
「ｓは秒。英語のSecond（セカンド）な」
「英語嫌い……」
予想通りの反応。
「俺もだ。単語ぐらい我慢しろ。というか、意味はどうでもいいんだ。質量はｍで、キログラム、ｓは秒で……って覚えろ」
「う、うん……」
で、単位だけ見てみると、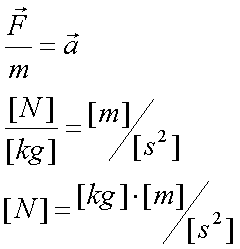

とまあ、Nの次元が分かる。
次元と言うのはつまり、長さ、重さ、時間がその物理量に対して何次なのかということだ。ま、あまりごちゃごちゃ言っても仕方ないから省略。

「次元……？　大介？」
「違う」
このボケ屋め……
「この次元は結構重要だからな。今は大した事ないと思うかもしれないが、この概念があるのとないのとではかなり違う」
次元を気にしていると、物理の理解が早くなる気がする。気がするだけだが。
「ちなみにニュートンは後からといってつけられた単位だ。１ｍと１kgと1秒に無理やり合わせた結果、新しい使いやすい力の単位、ニュートンが生まれたわけだ。知ってると思うが人名な。人名由来の単位は大文字。それ以外は小文字」
「後からつけられた……？」
わからない様子の稲穂。
「うーん、じゃあ説明しておくか」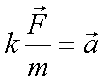

そもそもこんな感じだったんだ。
力の大きさの単位なんて、決まってなかったから。この法則が発見されたの、すげえ昔だし。基本的な意味はさっき説明した通り。加速度は力に比例して質量に反比例します。と。
ｋってのは比例定数で……まあ、説明すると長くなるから省略。とりあえずこのｋで法則性を保ってたわけだ。だが、使いにくい。いちいちｋなんてつけていたらな。
で、メートルとか秒とかキログラムとか決めた後、Fの中にこのｋを含ませてしまったわけだ。恒久的にｋ＝１になるような単位設定にした……それが[N]ニュートン。ってわけだ。

「う、うーん……」
一通り説明を終えると、稲穂は唸っていた。
「分かり辛いか？」
「うん、ちょっと……」
まあ、俺も説明が上手いってわけでもないしな……
じゃあ極端な例をあげるとするか。
「つまりだ。それまでの力の単位が『きつね』だったとしよう」
「き、きつねっ？」
驚く稲穂。ぴくぴくと耳が動く。
気になって仕方ない。
「そう。で、1kgの物体に、１m/s^2の加速度を与える力が0.07832きつねだったとしよう」
「う、うん。変な数だね……」
神妙にうなずく稲穂。
そんなに真面目に聞かれてもなあ……
「変だろ？　運動方程式は」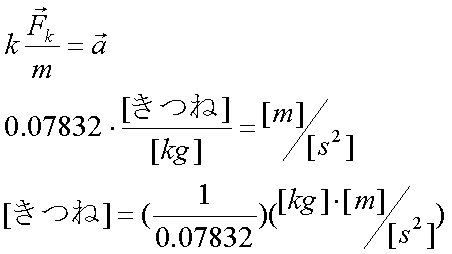

ますます変になる。使いにくい。だから考えた。
0.07832きつねが１ニュートンなら使いやすいんじゃねーの？　と。そうすると、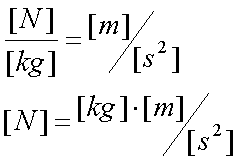

「こうなる。旧単位『きつね』は引退……まあ、実際なんていう単位が使われてたのかは知らないが。さらに俺らはMKS世代だからな」
「えむけーえす？」
首をかしげる稲穂。
今説明しても仕方ないんだけどな……
「俺らの先生はcgs単位系っての使ってたの。センチメートル、グラム、セカンド。俺らのMKSは、メートル、キログラム、セカンド」
「……わかんない」
そらそうだろう。もう少し物理の問題に慣れないと。
「ま、勉強には直接関係ないからいいさ」
この話にはあまりこだわらず、さっさと次の話に移った。
「でだ、運動方程式でずいぶん時間がかかったが最後は作用反作用」
これもまあ、単純な話だが。
「まああれだ。俺が稲穂を押すとするだろ？　そしたら俺も力を受ける。壁に全速力でぶつかると、ばしーんと跳ね返されるだろ？　あれも作用反作用。自分が力をかけるとそれと同じ大きさの力が返ってくる」
「それだけ？」
案の定、稲穂も拍子抜けしたような表情。
「ああ、それだけだ。基礎なんてそんなもの。後で使うから」
まあ、3法則はセットだしな……
「ふーん……」
「まああれだ。宇宙でボール投げるとずっと飛んでいくだろ？　で、投げたほうも反対側に飛んでいく。回転運動は別にして。あれは初歩的な法則によってるわけだな」

それから、力の大きさや方向は、複数の力がかかる場合はその和……全部足したものになる。たとえば、上と下へ同じ大きさの力がかかってる場合、見た目上力はかかってないよな？　だから力は０になる。
右と左に力がかかって、右への力がちょっとだけ強かったら、右に小さい力がかかっているように見える。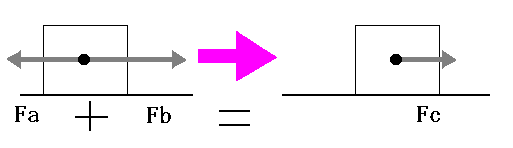

Fcの大きさはもちろん、Fb－Faな。
この辺はまた、ベクトル教えるときにやるから。

じゃあ問題。
5kgの物体がある。初めは止まってたんだが、力を加えて4秒で10m/sになった。
かかった力はいくらだ？

「え……うーん。４秒で１０メートル毎秒」
こういうとき次元……というか単位をみれば一発なんだがな。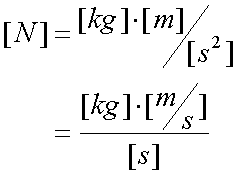

こういう構成。
だから、5[kg]に10[m/s]を掛け、４[s]で割ればすぐ出てくる。
えーっと、25/2[N]か。半端な数にしちまったな。

一方稲穂は、まだ唸っていた。
「ｍは5kgでしょ……aは、うんと」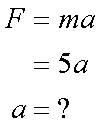

「4秒で10m/sになるんだよね……」
「加速度は、一秒で何m/sになるか……だぞ」
「うん……4秒で１０……」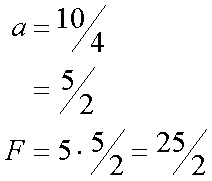

「これ？」
「正解。別に12.5とか直さなくていいぞ」
意外とやるじゃないか。

「わかったか？」
「うん……なんとなく」
ま、そのうち慣れればいいさ。
「運動方程式に関してはとりあえずここまで。後はまた次だな」
次は……重力と運動かな。ベクトルはその後ってとこか。

学習プランを胸に、今日の勉強はお開きとなった。

戻る