Fox ＆ Mathematics 　　　　　〜べんきょう、しよう〜 　　ベクトルの話 遅い。 いつもなら勉強が始まっている時間なのに、まだ稲穂は来ない。 「なにやってんだ……」 佐倉さんがついてるから心配はないだろうが…… 「…………」 いや、余計に心配かもしれない。 佐倉さんもあれで結構まともじゃないとこあるしな…… ピンポーン 心臓に悪い音量のインターホンが鳴った。 「来たか」 よっこらせと腰を上げ、玄関へと向かう。 ひんやりしたドアを開けると、目の前にフリフリの服を着た女の子が立っていた。 「こん……ばんわ」 何も言わずにバタンとドアを閉める。 ……さて、明日の予習でもするか。 「わー、閉めないでよ！」 なにやら外でわめいている奴がいるようだ。 「……誰だお前」 チェーンをかけて、ドアを少し開けた。 「耳見て分かるでしょ！　私よっ！」 どうも声と口調は稲穂っぽい。ついでに顔も。 だが、首から下は俺が今まで見たことのない人間だった。 「俺にそんな服を着てくるような知り合いはいない」 それを聞いた稲穂もどきは、泣きそうな顔になる。 「ううー……私だって『おかしいかも』って言ったのよ！」 ふむ、とすれば、こいつにこんな服を着せた犯人は絞られる。 「佐倉さんか……」 「ゆかりちゃんよ……」 ひゅうっと風が吹いた。 「…………」 「…………」 じっと見詰め合う俺たち。 なんだか知らないが、心が通じ合った気がした。 俺は一度ドアを閉めると、チェーンを外して再び開けた。 「まあ、入れよ」 「うん、ありがと……」 「……あまり落ち着かないが、とりあえず時間も過ぎてるし始めるか」 「うん」 狐の耳を立てて、フリフリヒラヒラの服を着て勉強……か。 多分有史以来この時この場所以外ないんじゃないだろうか。 「今日のテーマはベクトルだ」 「ベクトルー」 分かってるのか分かってないのか、稲穂が復唱する。 「まずはベクトルの定義。大きさと、方向をもつ量のことだ。終わり」 「大きさと方向……例えば？」 「例えばだな……物体が飛んでいく速度。これは方向と大きさがあるよな」 「ふんふん」 北に3m/sとか、下に7m/sとか。 「分かりやすくいえば、矢印で表されるようなもののことだ」 「矢印……」 紙に書いてみる。 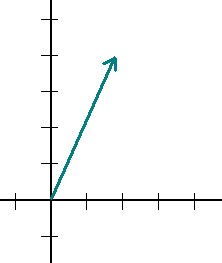「長さが大きさで、向きは矢印の方向。この方向にこのぐらいの速度で飛んでますよーと」 「んー……ああ、そうか。速度は矢印で表せるね」 速度や、力なんかもこうなる。 「逆に、温度や質量なんかはベクトルじゃないよな」 「うんうん、矢印で表せないもんね」 意外と物分りが良いな。 「そういうベクトルではなく、大きさのみ持つ量を、スカラーという」 「スカラー……モルダー？」 「それはスカリー」 「ちぇ」 口を尖らせる稲穂。 一体なにが残念なんだ…… 「ま、それはいいとしてだ。ベクトルの足し算引き算について」 足し算はこう。 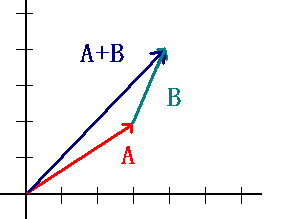ま、矢印の先っちょからまた足せばおしまいだな。終着点に原点から伸びていけばいい。 引き算……の前に、マイナスのベクトルの定義。 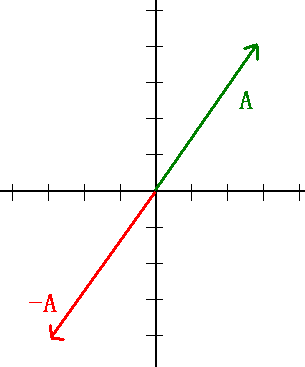マイナスのベクトルは、大きさが同じで方向が正反対を向いているベクトルのことだ。 で、引き算。 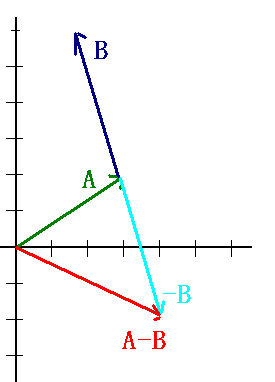足し算と同じように考えた場合、マイナスのベクトルを足してやればいいことが分かる。 一応、式で表すとこうな。 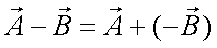「ふんふん。マイナスを足すんだね」 「ああ、そうすれば引いたのと同じだからな」 次に、ベクトルの表し方。 普通は上に「→」乗っけたり、文字を太くしたりするんだが……今回は「→」で統一な。 で、ベクトルの状態だが……まあ上のようにグラフで表すのが手っ取り早いが、各成分の大きさを現すだけでもうベクトルのすべてが分かる。 こんな風にな。 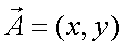こうすれば、もっと次元が増えても対応できる。 あんまり増やしても混乱するだけだから、３次元までにしておく。 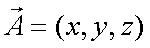こすうれば、足し算も引き算も簡単だな。 ここではベクトルAとベクトルBの各成分を、次のように表すことにする。 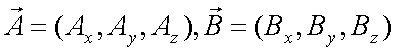そうすると、 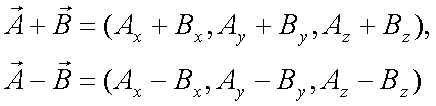それぞれの成分を足したり引いたりしてるわけだ。 それから、縦棒で挟んだものは絶対値。方向は考えずに大きさをだけを現したものだ。 で、それは矢印なしの文字で表されたりする。 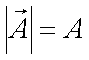「んー、何となく分かった」 じゃあ、次はベクトルの掛け算。 ここからは３次元でいくぞ。 ベクトルの掛け算には、実は２種類ある。それが内積と外積だ。 それぞれ、スカラー積、ベクトル積なんて呼ばれることもある。 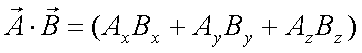まあなんというか、各成分をかけて足し合わせたわけだ。 あと、こういうのでも内積は求められる。 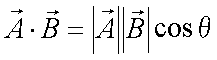θは二つのベクトルの成す角な。 これから分かるように、２つのベクトルが直角だと、内積は０になる。Cos90°は０だからな。 あと、各ベクトルの大きさは内積で定義されて、 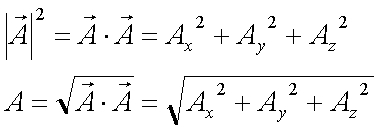ま、三平方の定理みたいなもんだ。 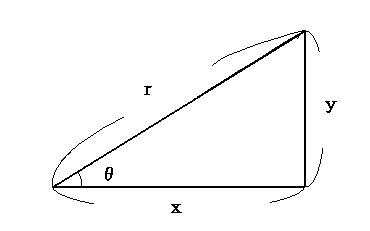ｒをベクトルだと思ってみろ。ｘとｙが各成分だとすれば、ｒの大きさを求めるとき…… 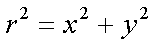「ほんとだ、似てるね」 「だろ？」 次に外積。 外積の定義はこう。 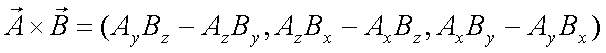ここで、「×」が出てくる。 普通は「×」が出てくると、まず外積だと思われるから注意しろ。 「……何これ」 予想通り、すごいものを見たという顔をする稲穂。 「外積」 「むちゃくちゃ分かり辛いんだけど……」 「だろうな」 まあよく見てみろ。 ｘ成分はｙとｚしか使ってないだろう？ 同じように、ｙ成分はｘとｚだけ。ｚ成分はｘとｙだけ使ってる。 それから、ｘ→ｙ→ｚ→ｘ→ｙ……という流れを頭に入れるとだな。 ｘ成分はｙ→ｚを使っている。だからAのｙからBのｚをかけて、AのｚからBのｙを引く。ｙ成分はｚ→ｘを使ってABのｘｚとｚｘ。ｚ成分も同じ。 まあこれは定義だから覚えるしかないな。 「うー……何か役に立つの？」 ……難しいとくれば『役に立つの？』か。 「実生活に役に立つかどうかは知らん。そんなこと物理屋には関係ない！」 言い切ったものの、俺自身まだ『物理屋』なんて言えるレベルでもないんだが。 「おお……」 とりあえず、稲穂は気圧せたみたいだからいいか。 「２本のベクトルを含む平面は必ず定義される」 突然話を再開した。 「どういうこと？」 首をかしげる稲穂。 「つまり……どう言えばいいんだ？」 難しいな……と、視界の端に割り箸が見えた。 ちょうどいいからこれを使おうことにしよう。 「稲穂。適当にこの箸を持って前に出してみろ」 「こう？」 右手と左手に一本ずつ、ハの字に箸を持つ稲穂。 「そうだ。その角度を維持したままで、二本をくっつける。くっついたところが原点。そこに……こう、紙をあてる」 ハの字がくっついて『人』になったその上に、レポート用紙を置いた。 「んー……うん」 「紙ってのはつまり平面だ。今箸は二本とも、平面に含まれてるよな」 ぴったりくっついている。 「ああ、うんうん」 納得の稲穂。 「じゃあ、ねじってみたらどうかな」 右のを縦に、左のを斜め下に構える稲穂。 「その角度を維持したままで、またくっつけて原点を作る」 言われたとおりにする稲穂。 そして、また紙をくっつける。 「あ、どうとでもなるね」 まあなんというか。くっつけることで原点をつくり、そこからのびる2本を軸だと考えて、平行四辺形みたいに歪んだ平面ができるというわけだ。 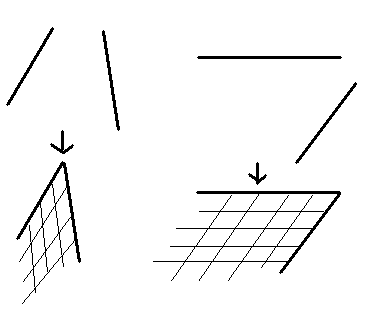ヘタクソな図で申し訳ないが、気持ちだけわかってもらえれば。 「うんうん。２本のベクトルは平面を作るね」 とりあえず納得した様子の稲穂。 「でだ。元の話に戻る。外積は、その２本のベクトルで作られる平面に、必ず垂直なベクトルになる」 稲穂の目の前に、またレポート用紙を取り出した。 「こういう平面があるとするだろ。その平面で作られる２本のベクトルの外積は、こうなる」 俺はその上に、えんぴつを立てた。 「へー、そうなんだ……あれ、でも垂直のって２本できない？」 「ああ、紙で言う裏と表な」 なかなか鋭いじゃないか。 「それはだな……まあ、教えるか」 計算したら出てくるが、方向だけすぐ知りたいときもあるしな。 「まず、人差し指を立ててみろ」 「こう？」 言われたとおり、ぴんと人差し指を立てる稲穂。 「そうだ。で、指先を上に向けたまま、反時計回りに一回転させてみろ」 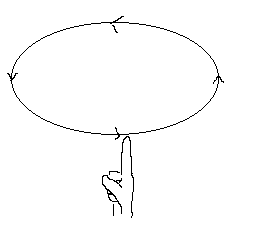ちなみに下にある物体は手だ。 「こう？」 くるりと反時計回りさせる稲穂。 「そう。それが基本だから覚えておくように」 世間では右ねじの法則とか言うが、俺は覚え方が違っていた。要は人差し指を上に向けたまま、円を描き……手前側で右に動いていくのがそれだと覚えている。 「……で、これがなんなの？」 くるくると指を回しながら、稲穂が聞いてきた。 「ああ、外積のA×Bがあるだろ？　このＡとＢの順番は意外と重要なんだ」 「ふんふん」 「２つのベクトルの原点を合わせて、AからBに向かって手を動かす……」 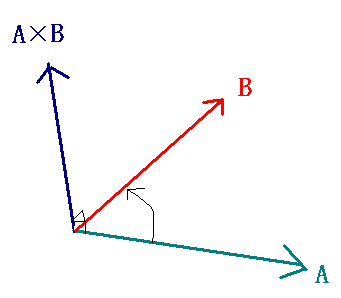こうだ。 で、これは反時計回りだから、上向きにベクトルが現れる。 さっき教えたとおりに指を動かしてみろ。 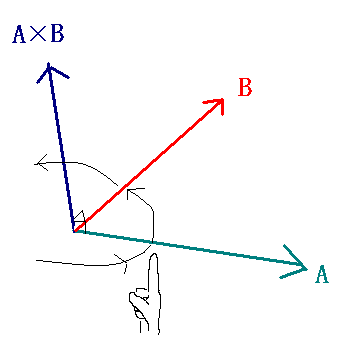AからB……ほら、指は上を向いたまんまだろう。逆にBからAだと下を向く。さっき教えた動きと反対だからな。 見て分かると思うが、外積の計算は結構間違いやすい。だから元の２本のベクトルのどちらかと、内積をとってみればいい。２本とも外積のベクトルと垂直だから、内積は０になるはずだ。 じゃあここで練習問題。 ベクトルA＝（−１，３，２）と、ベクトルB＝（４，２，６）がある。この二つのベクトルの成す角はいくつだ？ 「えっと……」 唸る稲穂。 「成す角が出てくるのは……」 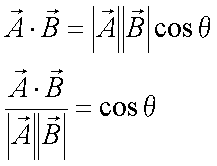「内積と絶対値は……」 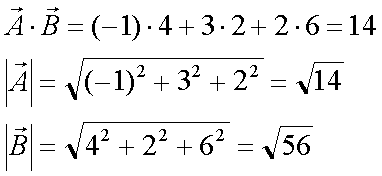ああ、ルートの中は掛け算しても大丈夫だ。 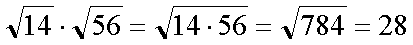と。で、ここからどうする？ 「えっと……」 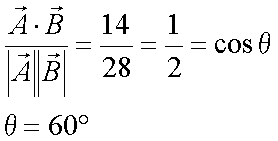「こう？」 オッケーだ。 じゃあちょっと難しいが、空間のグラフを書いてみる。 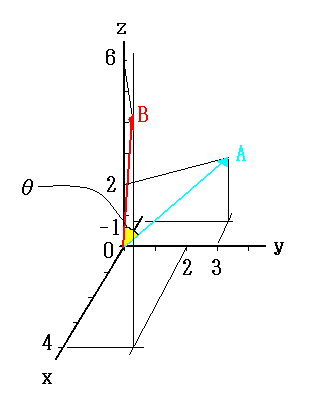恐ろしく分かり辛いが、気持ちだけでも分かってくれればいい。 次の問題。Ａ＝（１，２，０）Ｂ＝（５，２，０） Ａ×Ｂを求めよ。 「が、外積だ……」 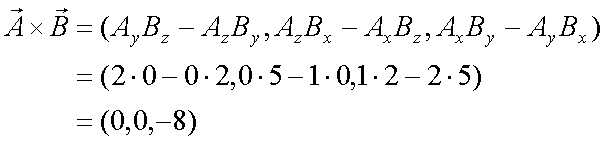「こう？」 さっきの公式とにらめっこしながら、稲穂が答えにたどり着いた。 「おっけーだ。2本ともｘｙ平面のみだったから、垂直な外積はもちろんｚ方向に伸びるよな」 「あ、ほんとだ」 「しかもその方向は……」 「下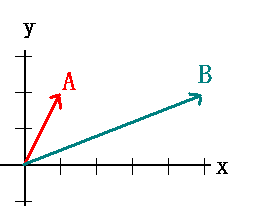！」 グラフに表すと、こうな。 ＡからＢに動かすと…… 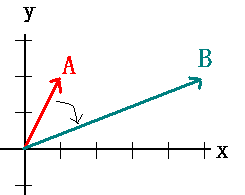こうなる。 さっきの基本の動きと逆だよな。 だから上を向かずに下を向く。紙の手前側がｚの正だから、紙の向こうへ向かうのはｚの負。 ほら、計算結果と合ってるだろ？ 分かると思うが、Ｂ×Ａの場合は、上を向く。だから、 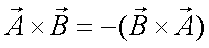ということが分かる。 ちなみに外積の大きさは、 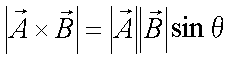で求められたりする。あまり使わないけどな。 「よし、今日はここまで」 「つ、疲れたー……」 そりゃあ、1日でやれるような分野じゃないしな…… 「まあ、しばらく時間空けるから、復習しておくようにな」 「うん、わかった。わかんないところあったら、聞きに来るね」 「おう」 ピンポーン 一息ついたところで、やかましいインターホンが鳴った。 「……誰だろ？」 首をかしげる稲穂。 「佐倉さんだろ」 と、俺が腰をあげるより早く、来訪者が勝手に入ってきた。 「こんばんはー」 妙なテンションに、 「…………」 疲れた稲穂はついていけず、 「…………」 俺は佐倉さんが一体何を言い出すのかと待ち構えていると、 「ねえねえ都君」 やたら嬉しそうに佐倉さんが話し掛けてきた。 「なんですか？」 すると佐倉さんは、フリフリの稲穂を指差してこう言った。 「惚れた？」 なぜだか知らないが満面の笑み。 俺たち二人は顔を見合わせると、 「「……はぁ」」 同時に仲良くため息をついた。 アンケートご協力お願いします 戻る