極限のお話

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　極限のお話

レポートが終わらない。
だが、
「ねー、達哉ぁ。勉強教えてよー、勉強ー」
周りで稲穂がわめき散らす。
「うるさいなあ……」
締め切り明日までなんだが……
俺としてはもちろんレポートを優先させたい。だが……
「勉強しよう、勉強」
稲穂は微塵も分かっちゃくれなかった。
「仕方ないだろ。やること終わらせないと」
半分ぐらいは終わったものの、まだきつい問題が残っている。
少し静かになったかと思うと、
「達哉遅いー……」
俺の手元を覗き込んで文句を言う。耳が顔に当たって邪魔だ。
「量が多いんだから仕方ないだろ」
そりゃあ、稲穂の例題みたいにさくさく解けるような奴ならいいが……
「うー……燃やすよ？」
「燃えたら勉強できなくなるぞ」
さりげなく恐ろしいことを言う奴だ。
「うー……」
相変わらず稲穂は唸っていた。
「はあ……」
一つ大きなため息をつく。
「……わかったわかった」
「え、勉強教えてくれるの？」
ぱっと表情が輝く稲穂。
「ああ、さっさと終わらせたほうが良さそうだからな」
まったく……横でなんだかんだと言われてたんじゃ、全然進みやしない。
さっさと稲穂を帰らせて、それからレポートに取り掛かった方が良さそうだ。

「今日のテーマは極限だ」
「極限？」
首をかしげる稲穂。
どうやらボケは浮かばなかった様子。
「まあ、なんというか説明するのが難しいな」

例えばこういう関数があるとして、ｘがどんどん大きくなっていったらどうなる？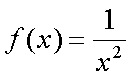

「んと……どんどん小さくなる？」
「そうだな。ものすごい勢いで０に近付いていく」

だが完全に０になることはないんだな、これが。
とはいえ、ほとんど０であるとは見なせるわけだ。
0.0000000000000000000000000001なんて100に比べればあるのかないのか分からないだろう？
で、そういうときにこうして表すわけだ。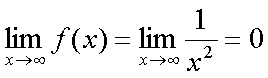

∞は見たことあると思うが、無限大の極限のことな。めちゃくちゃ大きい数ってイメージ。
でまあ、普通の関数でもこういう風に表せる。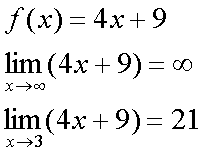

あまり「＝∞」とは書きたくないな。気持ち悪いから。ここでの「＝」は限りなく近付くって意味な。
「∞」ってのはそういう数じゃなくて、あくまでなんか知らんがでかいものだから。
で、次。ｘがどんどん3に近付いていくんだから、ｘに３を代入して２１だよな。終わり。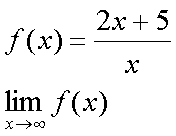

この場合はどうなるか。普通は分母が無限に飛んだら関数は０に近付いていく。だが、この場合は分子にもｘがある。ということは、約分ができる。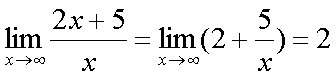

２項目がｘ分の５で、ｘが無限に飛ぶと、この部分は０になるよな。で、残るのは前の２だけ。ってわけだ。
まあ、やれるだけやってから変数の部分を見ろってことだ。
分母が０に近付くなら数は無限に、分子が０に近付くなら数は０。
分母が無限に飛ぶなら数は０。分母が０なら数は無限だ。

「うー、もう少しゆっくり……」
「よし、じゃあ例題な」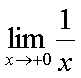

「プラスゼロ……？」
「そうだ。まあやってみろ」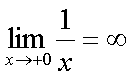

「こう？」
「正解。じゃあ次」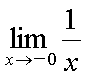

「マ、マイナスゼロ……さっきと同じじゃないの？」
「同じじゃないんだな、これが。まあグラフを見てみろ」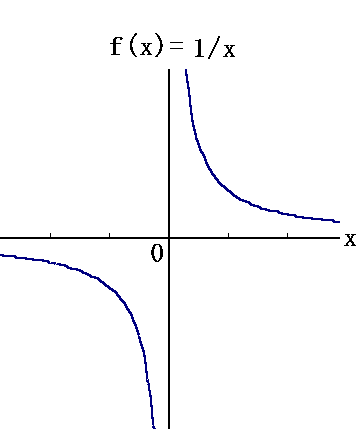

「あー、下に伸びてるんだ」
グラフを眺めて、稲穂がつぶやいた。
「そう。ｘの＋側から0に近付くのと、－側から0に近付くのとでは、正反対なんだ」
「じゃあ……」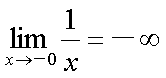

「これでいいの？」
「OKだ」
嬉しそうな稲穂。
まあ、問題が解けて嬉しいってのはいいことだな……
「そういえば達哉」
「ん？」
「前に０の０乗を解くって言ってなかったっけ」
あー、そんなことも言ってたような気がする。だけどあれ、ロピタル使わないと解けないからなあ……あと対数も。
「ああ、それな……実は微分をやらなきゃ無理だった」
「ええー……」
不満そうな稲穂。そんなに知りたいのか……答えは1なんだが。
「我慢しろ。ものすごい定理だから。もう少しの辛抱だ」
物事には順序ってもんがある。
……まあ、それをすっかり忘れていたのは俺だが。
「ううー……」
やっぱり稲穂は不満そうだった。
「気を取り直して次の問題」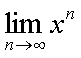

問題をじっと見て、稲穂が口を開いた。
「え、これって無限に行くんじゃないの？」
ふふふ、そう来ると思ったぜ。
「甘いな。何乗しても変わらない数があるだろう」
と、ヒントを出してみる。
「何乗しても……あ、１？」
その通り。１は何回１を掛けてもずっと１のままだ。
「当たり。あと、掛ければ掛けるほど小さくなっていくものもある……」
「えー……なにそれ？」
どうもわからない様子。小数を忘れているか……
「ま、模範解答はこれな」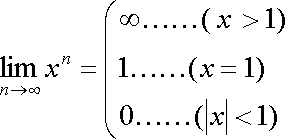

「絶対値だ……|x|＜１ってことは、－１＜ｘ＜１ってことだよね？　ああ、0.5に0.5かけたら0.25で、ずっと小さくなっていくね」
やっと理解した様子。
「そうだな。ちなみにｘ＜－１のときは解を持たない。収束しないからな」
「そうなの？」
「考えてみろ。－1に－1掛けたら１だろ？　また－1掛けたら－1だ。で、また－1掛けると１……－1と１の間を行ったり来たりってわけだ」
「あー、ほんとだね。じゃあマイナスのときは解なしでいいんだ」
うんうんと頷く稲穂。
というわけで次の問題に行くか。
「次はテクニックがいる問題だ」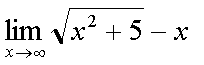

「無限……だけど引いてるんだ」
「ああ、どうする？」
なんというか、理想的なつまり方するな、こいつ。思う壺って感じで嬉しいぞ。
「ルートの中は２乗だから、大きさはどっちも同じくらい……あー、でも……わかんない」
白旗の稲穂。
「じゃあ、解答」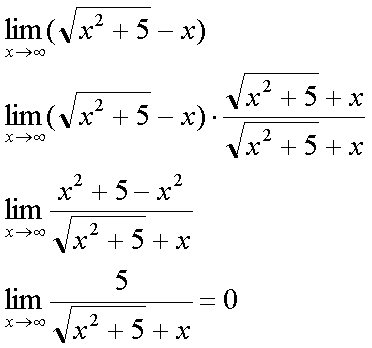

「こうなる」
「な、なんかすごいことやってない……？」
おびえた様子の稲穂。
「別にすごくないぞ。２段目でやってることは、１を掛けただけだ。分母と分子が同じなら１だろ？」
かなりいかつい式だが。まあ１は１だ。
「う、うん……」
「で、３段目ではそれを掛けている。（a+b）・（a－b）はa^2－b^2だろ？」
「あー……あー、あー。分かってきた。ｘの２乗はなくなるね」
じわじわと納得し始めた稲穂。
「で、分子を５だけにすると、分母は増えていくばかり……数は０になると」
単純な話だな。
「ま、面倒なことをやったが、ｘが大きくなっていくと、５は無視できます。ルートｘの２乗はｘです。ｘを引くと０です。終わり。でもいいんだけどな」
種明かし。でもこうやるのは数学屋さんは嫌うんだよな。神経質だから。物理屋さんは適当な近似でOK。なんとも気楽な学問だ。
「ほ、ほんとだよ……それでいいじゃない」
「ま、そんなことやっても面白くないだろ？」
「そりゃまあ、こっちの方が面白いけど……分かりにくいよ」
面白いか。まあ数式をいじるのは確かに面白いな。
「はは、じゃあ次」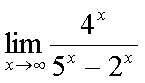

「ん……０になりそうな気もするけど……ヒント」
お。なんとか自力でできそうか？
「ヒントか……まとめてみな」
「まとめる？　うーん……」
わからない様子。まあ、まとめるって言っても抽象的だからな。
「絶対値が１より小さい数は０に収束するだろ？」
「うん」
「だから……」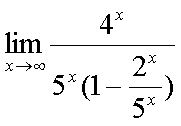

ノートに書いてみる。
「この後どうする？」
稲穂は変形された式を凝視する。
「うん……と、分子と分母はｘ乗でまとめられるよね……」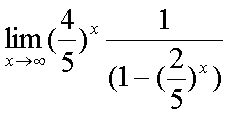

「前の方は収束して０……後ろの方は分母が１－０になるから１で、だから１か……掛けると０？」
「正解。答えはゼロだ」
やるな、稲穂。
「はあ、難しい」
息をつく稲穂。まあ、ここまでやれれば上出来だろう。
「じゃあ次で最後な」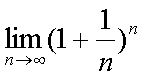

「……無限だから１＋０で、何乗しても１じゃないの？」
固まる稲穂。
「ｎ乗するが、中身も１じゃないぞ。しつこくしつこく掛けていけば、それなりの数になるかもしれないぞ」
と、いじめてみる。
「うう……でもこれ、どうしろっていうの……？」
「さあな」
証明した気もするが、忘れた。覚える必要も余りないし。
「さあなって……なにそれ」
「収束することはするんだが、困ったことに変な数なんだ」
「変な数？」
いぶかしげな顔の稲穂。でも変な数としか言いようがないしなあ。
「ああ、こんな数になる」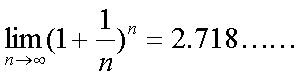

「点点点……って、なによこれ」
「ずっと続く……らしい」
この後は忘れた。２だか３だかだった気もするが、あんまり無責任なことも教えられない。
「え、なんで？」
「仕方ないだろ。まあ深く考えるな。で、これはこう定義されている」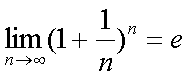

「いー？」
「いー」
「……なにこれ」
eをぐりぐりなぞりながら、稲穂が聞いてきた。
「円周率を『π』と書いてパイと読むことは知ってるか？」
「えっと……そうなの？」
知らなかったのか、こいつ……
「円周率は3.1415……で終わりはない。今のところ」
「うん、そうだよね」
今日もどこかのコンピューターが、がりがり計算しているはずだ。
「３でも3.14でも不正確なんだ。だからπで表す」
あ、やべ。ラジアン教えてない。微分の前にはラジアン教えておかないとな……
「ふうん。で、同じようにeなんだ」
「そういうことだ。このeって奴なんだが……実は無茶苦茶便利なんだ」
「おおー」
よく分かってなさそうだが、驚く稲穂。
「でもそれが本領を発揮するのはもう少し後な」
主に微積だな。あ、自然対数でも使うか。
「じゃあ今日はここまで」
はあ、なんか疲れた。
「頑張ったねー」
にこにこ笑う稲穂。嬉しそうだな、こいつ。
「まあな」
例題が多かったからな……
自分で問題を作るのは結構苦労するな。

ピンポーン
やかましいインターホンが鳴り響く。多分佐倉さんだ。
「はいはい」
玄関を開けると、予想通り佐倉さんが立っていた。
「お疲れ様ー。もう終わったかな？　お菓子持ってきたよ」
タイミングばっちりじゃないか。
「どうぞ。上がってください」
「お邪魔しますー」
佐倉さんの差し入れは、チョコレートがコーティングされた餅だった。
「変な食感でおいしいんだよ」
「そうですか……」
まあ、頭を使った後は、甘いものがありがたいわけだが……
「うん、おいしー」
幸せそうな佐倉さん。
「変な感じだね。甘くておいしいけど」
と、稲穂。
「こんなのどっから仕入れてくるんですか……」
と、聞いてみたところ、
「うん、おいしいから」
全く答えになってないぞ……
まあ、そんなこんなで三人でまったりとした時間を過ごしたわけだ。
だがしかし。
佐倉さんと稲穂がまったりし過ぎて、なかなか帰ろうとしなかった。むげに追い出すわけにも行かず、三人でお茶まで飲んだりして。
日付が変わるころ二人は隣へ帰り、やっとこさ俺はレポートのことを思い出した。
結果、2時までレポートに取り掛かる羽目に……
やっぱり最初、稲穂を待たせりゃ良かった。くそう……

戻る