対数のお話

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　対数のお話

晩飯を終え、勉強時間が始まるまでの間。
のんびり漫画を読んでいると、稲穂が話し掛けてきた。
「ねえねえ、達哉とゆかりちゃんって仲良いよね」
えらく唐突だな。漫画を置くと、稲穂のほうを向いた。
「そうか？　まあ、そうだな……」
「すっと前から知り合いだったの？」
「いや、そうでもない」
まあ、２年半ぐらいだったら、ずっと前というほどでもないな。
ちなみに今日、佐倉さんは研究室に行っていて遅くなるらしい。
「初めて会った時って、どんなだったの？」
どんなもこんなも、余り変わってはいないんだが。
「んー、話してやろうか」
「うんうん」
楽しそうに笑う稲穂。
そして俺は、大学１年の４月のことを思い出していた。

引越しを終え、一息ついてから携帯に電話があった。
母だ。曰く『お隣に挨拶するように』と。
俺の部屋は２０１。隣といえば２０２。幸運なことに（？）一つだけだ。
こんなこともあろうかと、荷物に地元の名物の饅頭を仕込んでいたらしい。これを持っていけということか……相手が饅頭嫌いだったら、またその時に考えよう。
ピンポーンとインターホンを鳴らす。
「はーい」
表札には『佐倉』とだけ書いてあるが、中から聞こえてきたのは女性の声だった。
ほどなくしてドアが開き、中から温厚そうな女の人が顔を覗かせた。
「隣に越して来た都です。いろいろとご迷惑おかけするかもしれませんが、よろしくお願いします」
「あ、はいはい。これはご丁寧にー……と、うちの大学かな？」
うちの大学……がどこを指しているのかは知らないが、とりあえず近辺には大学は１つだ。
「えっと……平安大学ですが」
「あ、じゃあ一緒だね。私は文学部だけど。佐倉ゆかりです。よろしく」
そうか、この人も同じ大学か……なんというか、心強いな。
「理学部物理の都達哉です……と、そうだこれ、お近付きのしるしに」
そう言ってビニール袋に入ったそれを差し出す。
「なにかな……あっ、草神饅頭！」
どうやら知っている様子。そんなに有名だったっけ？
「一応地元なんで……こういうお土産の方がいいかと思って」
他に目立った名産がないというのもある。そもそも観光地じゃないしな……
それだけに、この人が知っているのが驚きだ。
とか思っていると、意外な言葉が飛び出した。
「というか、私も草神」
「え、本当ですか？」
ど、同郷の人に饅頭送ってしまったのか……
「うん、御崎原高校だよ」
「あ、俺は志乃上高校なんですけど」
ちなみに、御崎原と志乃上は隣の駅同士だったりする……
「へえ、近いね。実家は？」
「実家はですね……」
とまあ、こんな風にして話がはずんで行ったわけだ。
それにしてもこんなところで同郷の人に会うとは……いや、進学している人は過去に何人もいるわけだが。平安大ぐらい大きな総合大学は近場にあまりないし。
しかし隣の部屋とは……

「ま、そんな感じだな」
話を聞き終えた稲穂が、何か言いたげだった。
「どうした？」
「……あのね、達哉」
意を決したように、口を開く稲穂。
「ん？」
そこからまた、思いもしない言葉が出てきた。
「私も前に草神に住んでた」
「まじか！」
な、なんてこった……
稲穂まで同郷……あ、いや、住んでただけで出身は違うかもしれないか。
「うん、志乃上の商店街に、神社あるでしょ？」
「ああ……って、まさかあそこに」
良く知っていた。幾度か遊びに寄ったこともある。というか……
予感は的中した。
「うん、いたときがあった。５年ぐらい前から2年間かな。修行みたいな感じで」
ガーン……
しかも俺の高校在籍時とちょっと、いや、割と重なってるじゃないか。
絶対１５メートル以内まで近付いたことがある。お、恐ろしい……
「なんてこった……」
草神から隆山まで電車で４５分。隆山からさらに電車で５０分。この沼崎市のはずれでこんな出会いがあるなんて……
世間は狭いというか、なんというか……

少々驚きを引きずりながら、勉強時間になった。
「今日は対数」
１回極限をはさんでしまったが、指数とくれば対数だ。
「対数？」
「対数。今までなかった概念だと思う」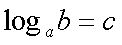

「……ろぐ？」
「ログ」
「なにこれ？」
予想通り首をかしげる稲穂。
まあ、定義としてはこうなる。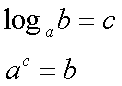

「？　どういうこと？」
ログってのは、aをbにするためにa自身を掛けなければならない回数ってことだ。まあ、何乗すりゃいいのかって話だな。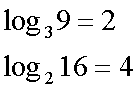

「あー、３の２乗は９で、２の4乗は１６だね」
「ああそうだ。で、左の小さい数を対数の底と呼ぶ」
「てい」
「ああ、底だ」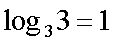

これはわかるよな。３は１乗で３だ。
上の式から分かることは、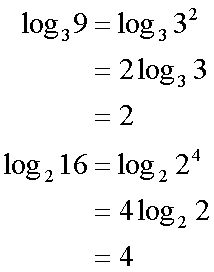

とまあ、こうなる。
何乗ってのは前に出せるわけだな。
「でまあ、この対数、他にもいろいろと決まり事はあるんだが……その前に一つ」
一応底の概念は教えたから、もういいか。
「うん？」
「３だの２だのを底に取ったが、ほとんどの場合そんなことはしない」
「そうなの？」
不思議そうな顔をする稲穂。残念ながら、それらの底を使う機会はない。大学に入って使った覚えもない。
「ああ、物理をやる場合は、底はeだ」
ネピアの定数。という名前があるらしい。
「eって……この前やったあれ？」
「そうだ。あれだ。不思議なことに、自然界はこれを元にして動いている場合が多い」
「そうなんだ……」
そうなんだよ。なぜかはしらないが。
だから、物理を学ぶ上では２だの３だの、そういう底はいらないわけだ……いや、いらなくもないかもしれないが、ほとんどeを使ってしまう。
「で、こう書き表す」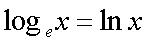

「ずいぶん省略したね」
「ああ、で、これは自然対数というもので『ログナチュラル』と読む。この場合は『ログナチュラルｘ』だな」
もちろん、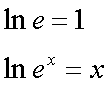

であることには変わりない。
でまあ、lnxのグラフはこんな感じになる。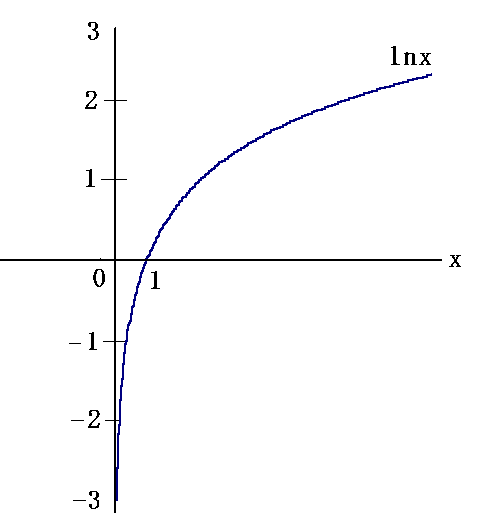

ｘが2.718あたりで１になってるだろ？
あと、ｘはマイナスをとれない。なぜかというと、eを何乗かしてマイナスになるものはないからな。
それは次のグラフからもわかる。
eのｘ乗と並べてみたグラフだ。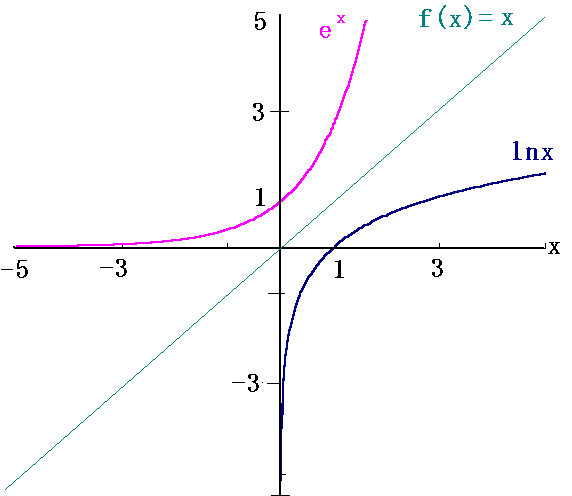

lnxがマイナスのxを取れない。eのｘ乗はマイナスにならない。
「そうなの？」
「３を何乗すればマイナスになる？」
じっとグラフを見詰める稲穂。
「んー……ピンクの線だから、無理だね」
早めに結論にたどり着いた。
「だろ？」
「で、eの０乗が１になるから、ln1は０になる。と」
別にeに限ったことではないが。
「うんうん。なんでも０乗したら１だったよね。その逆なんだ……分かりにくい」
「まあ、あっさり分かられても困るんだが」
でもこれがないと不便なんだよな、いろいろと。
「あと、指数の性質から導かれることは」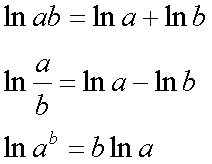

「この３つを覚えていればまあなんとかなるかな」
自然対数だけでなく、あらゆる底に関してこれは成り立つが。
「なんか適当だね」
「そういうわけじゃないんだが……」
底を変換する方法もあるんだが、自然対数しか使わないから別に教えなくても良いや。
あとは、イメージとして……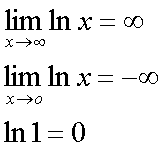

この３つぐらいはぱっと出てこないとな。

さて困った。これ以上教えることもないぞ。
時計を見るとまだ時間はある。
「どうしたの？」
稲穂が不思議そうにこちらを見る。
ふりふり揺れる尻尾が気になって仕方ない。
「いや、例題でもしてみるか」
「うん」

じゃあまず最初。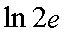

「うーん……分解すればいいの？」
「ああ、とりあえずやってみな」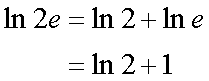

「こんな感じ？」
「正解。簡単だよな」
うーん、センターの問題でもやってみるか……
過去の新聞あったか……？
「ちょっと待ってな」
「うん」
あ、あれだ。確か下駄箱に敷いてたんだ。靴の匂いが取れるらしいから。なぜセンターの問題にしたかは、あてつけというか、過去の恨みと言うか……
発見。
対数の問題は……お。あった。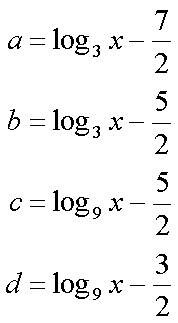

ｄ＝０となる場合を求めよ。
「ｄ＝０かあ……えっと」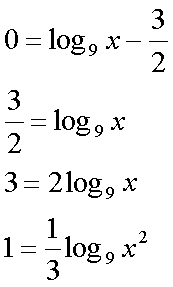

「3分の1乗……」
「ｘ＝の式に直して、両辺3乗して、ルートを……」
と、ここまで言ったら答え教えてるようなもんか。
「あ、わかった」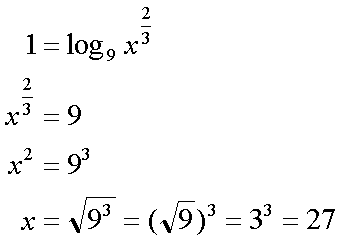

「OK。なかなかやるじゃないか」
「えへへ……」
照れる稲穂。ぱたぱた耳が動く。気になって仕方ない。
しかしまだまだこれからだ。

次に、abcd>0となる場合を考える。
a,b,c,d,全てが負となる場合は……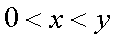

である。ｙを求めよ。
「全部負なんだよね……じゃあ、それぞれ……」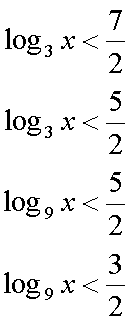

「だよねえ」
「ま、そうだわな。引くほうがでかけりゃ負になる。次は、ログの中に入れてみな」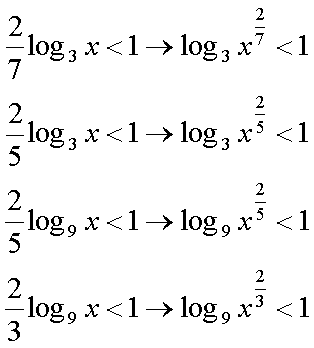

「よし、じゃあ、底とｘの関係式。1より小さくなるんだから……」
ｘの何乗ってのが底より小さくなれば、値は１より小さくなる。

よし、まあちなみに、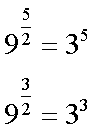

こうなる。
この中で一番小さいのは？
「えっと……2番目かな？」
「だな。2番目を満たしていれば、全部負になる……全部代入でやってみな」
ちなみに、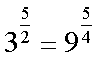

だ。一応な。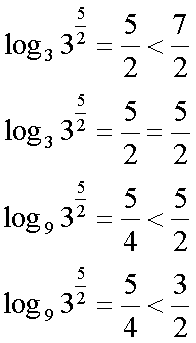

「あ、おっけー、おっけー」
喜ぶ稲穂。
「だな。ってことで」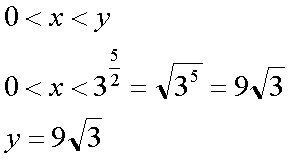

「となるわけだ」
スピード勝負のセンター、本番はあんまりのんびりやってもいられないが。
「次。abcdのうち、２つが正で２つが負の場合のｘの範囲」
「ええと……どれが早く正になるかな」
着眼点はなかなかいいな。
「2番目は決定として……あと１つ……」
「０になるのを考えてみろ」
「０……」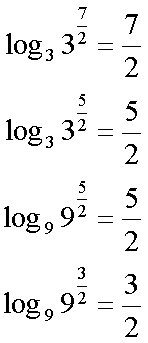

「これで０だよねえ」
「だな。あとは、数値を比較してみると……」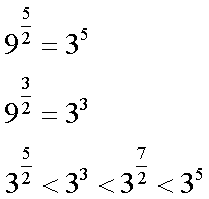

「ふんふん。じゃ、次に正になるのは4番目！」
正解。
「だな。で、この問題は範囲を求めろだから、上も当然決めなきゃならない」
「次は1番目の奴でしょ？　だから……」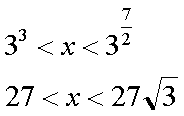

「センターはここまで書くように」
稲穂が書いた１行目に、2行目を書き足す。
「はーい。普段はいいの？」
「まあ、高校のときはいるかもな」
大学では大体放置だが。
「ふうん……」
分かったのか分かってないのか。稲穂がうなずいた。
「最後の問題。全部が正になるとき」
「そんなの簡単だよ。残った奴でしょ？」
あさり答える稲穂。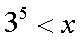

「えっと、９掛ける９掛ける３は……８１かける３で……」
必死に筆算しているが、３に８掛けて１に3掛ければすぐだ。
「２４３な。終わり」
稲穂が筆算を終えると同時に、答えを言った。
これで大問１の半分を理解できたって訳だ。
「はー、結構長い道のりだねえ」
息をつく稲穂。
まあ、本格的な問題だしな……
「まあ、こんなのは10分で済まさなきゃならないわけだが」
「ええっ！　そうなの？」
尻尾を立てて驚く。気になって仕方ない。
「ああ」
多分。
多少オーバーかもしれないが、さっさと解くに越したことはない。

「はぁ、疲れたー」
カーペット敷きの床に、ばったり倒れこむ稲穂。
「ん、今回は良くやった」
と、誉めてやる。
「さて、次は三角だな」
それにしても物理やってないな……
「え、この前やったんじゃないの？」
「応用編」
大体この前って概念やっただけじゃないか。三角は奥が深いんだぞ。
「ふーん……」
分かっているのか分かってないのか。
まあ、多分分かってないんだが。
その後はやっと微積……か。やれやれ。
まだまだ先は長そうだ。

戻る