微分のお話

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　微分のお話

いい加減暑くなってきて、授業にも身が入らない。
なんて言う奴もいるが、冷暖房完備の教室で何を言ってるんだか。
暑さ寒さで身が入らないようじゃ、どうしようもないな。
というわけで今日の授業は終了。できれば校舎から出たくないな……
「大変だ、都」
「ああ、そりゃ大変だな」
隣に座っていた米崎。もうすでに帰り支度は万全だ。
「まだ何も言ってないだろ……」
お約束じゃないか。今更そんな呆れ顔になられても……
「で、何が大変なんだ？」
「もうすぐテストじゃないか。テスト」
「あー、そういえば先生がそんなこと言ってたなあ」
いつの間にやらもう７月。
稲穂が来て１ヶ月少々。だったっけ？　正確な日付は忘れたなあ……
「何落ち着いてるんだお前。英語と量子と統計と、電磁気と原子だぞ！？」
「前3つはともかくとして、後ろの2つは去年お前が落としただけだろうが」
ちなみに俺はちゃんと単位をとった。
「それはそうなんだが。いやしかし、量子と統計だぞ？　どうするんだよ」
「どうするって……普通に勉強するさ」
「なんか余裕だな、都」
何でそう怪訝な顔になるかな。普通に勉強する以外の方法があるなら教えてもらいたいもんだが。
「いや、別に今から焦っても……」
「裏切り者め！」
指を差すな。指を。
よく分からんが、授業が終わって開放感に浸ってるんだろう。多分。
次の授業は休講だしな……久しぶりに午前中に帰れる。

外に出てみれば、やっぱりくそ暑かった。
「そういやどうだった、映画？」
「あー、面白かったぞ」
月並みだが。
面白かったかどうかと聞かれれば、面白かった。
「渡してから思い出したんだが、ばりばりの恋愛モノじゃなかったっけか」
「そういうことは早く思い出してくれ……」
まったく……
まあ、お陰で普段見ることのないジャンルの映画を見れたわけだが。稲穂も楽しめたみたいだし、まあ良しとするが。
「そうか。面白かったのか、そりゃあ良かった」
そう言って笑う米崎は、まあいい奴だ。
米崎と初めて話したのはいつだったか……多分１年の実験の時。同じ班のメンバーだったからだろうけど……なんというか、波長が合ったんだろうなあ。
勉強も意外と真面目だし。
「ん、どした？」
「いや。まあ再履がんばれよ」
真面目なだけに、落としたのが不憫なんだよなあ……
「おう。任せとけ。あ、俺本借りてくから。じゃあな」
気付けば図書館前。テスト前はやっぱり利用者が増えるようだ。
「涼しいからって寝るなよ」
「分かってるって」
「じゃあまたな」
そう言って図書館の前で米崎と別れた。
暑いな……早く帰ろう。

帰ってくると、部屋が地獄だった。
窓閉めたままだったか……
決死の覚悟で窓を開けると、たまらず隣の部屋に避難した。
あそこにいるのは、無理だ。
「達哉、帰ってくるの早いんだね」
佐倉さんの部屋には稲穂が一人。
「んー、休講になった」
避難してきた理由を話したところ、いたく同情してくれた。
佐倉さんはゼミのため大学らしい。
基本的にうちのアパートは風通しがいい。俺の部屋ももう少しすればなんとか生きていける環境になると思うんだが……
「普段帰ってくるのは夕方だけどな」
「ふーん、そうなんだ……」
テーブルの上を見ると、なにやら数式の書かれた紙。
どうやら復習していたらしい。
「達哉、時間あるの？」
「ああ、すげえ暇だ」
テスト勉強しなきゃいけないんだろうが……やっぱり直前にならないと身が入らない。
「じゃあ勉強しようよ」
そう言って、どこからともなく稲穂ノートを取り出す。
「お、やる気満々だな」
「うん。今日あれだよね。格好いいやつ！」
格好いいやつ……まあ、そうだな。
「ああ、そうだ」
ずいぶん楽しみにしていたみたいだからな……
どうも稲穂は「格好いい」という言葉に弱いようだ。
まあ特にすることもないし、勉強開始するか。

というわけで微分だ。
具体的に何するかっていうと、傾きを求めるんだ。
なんか適当な関数があって、そのある点での傾きを求める。それが微分。
適当な関数f(x)があるとする。んで、そのグラフがこんなのだとする。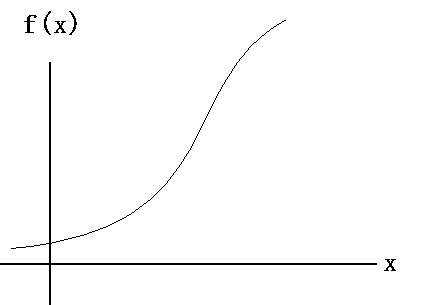

このグラフの中で、どこか２点間の傾きを調べる。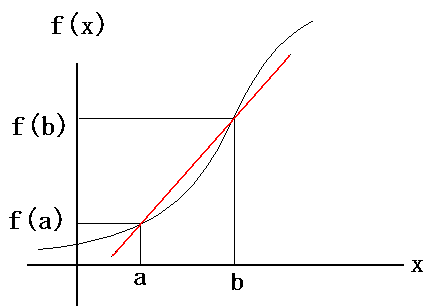

こうなるよな。赤い線が傾き。
ああ、言ってなかったかもしれないが、f(a)はf(x)のxにaを代入したやつ。F(x)=x+3のとき、F(2)=5みたいにな。
でだ、この赤い線の傾きの値を実際に求めると、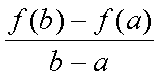

こうなる。ｘの差でyの差を割った形な。
ここまでは分かるな？
で、本当に求めたいのはこんな２点間の傾きじゃなくて、ある1点の傾きなわけだ。
でまあ考えた結果、bとaがすげえ近くにあれば、ほとんど1点に見なせるんじゃないかと。b－a=hとおいて……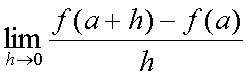

こうなる。これが微分の定義式みたいなもんで、ある点aを任意のｘとすると、

『f'(x)』のようにダッシュをつけて表すこともあるし、2番目の式みたいに、『df/dx』と書いてｘで微分していることを示すときもある。

「ｄ……？」
「ｄだな。英語で微分はDifferentiationだから、多分それだ」
違う気もするが。いや、きっと違う。微小変化のｄだ。
博識に見せかけて、実は英語のテスト範囲だから覚えていただけだが。
「結構重要だぞ。微分してますって合図だから」
「合図……」
言ってから気がついたけど、積分でも使うじゃないかdx。
……まあいいや。それはその時に。

でまあ、実際に計算してみる。
おなじみ二次関数で代入。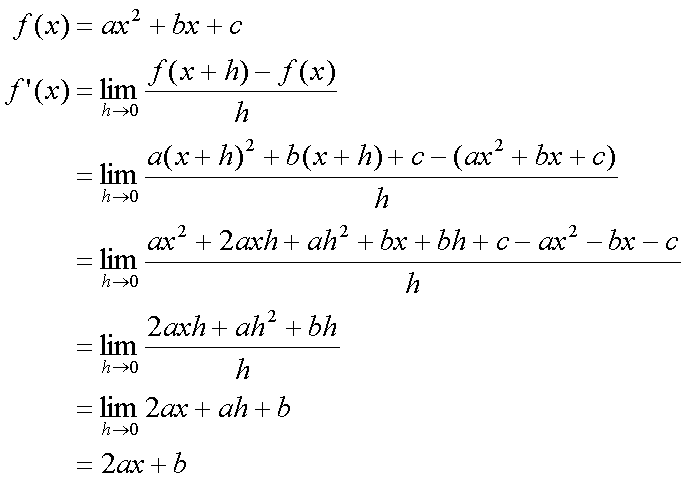

「えっと……開いて、同じ数を引いて」
指でなぞりながら、じっくり式を追っていく稲穂。
「ｈで割った」
「うん、それから……ｈが０なんだね」
つまり、ｈのある項は消える。消えるというか、ほとんど０だから無視してるだけなんだが。
「そう。残ったのは２axとb」
「ふーん……なるほど」

一般的なｘのｎ乗についてやってみる。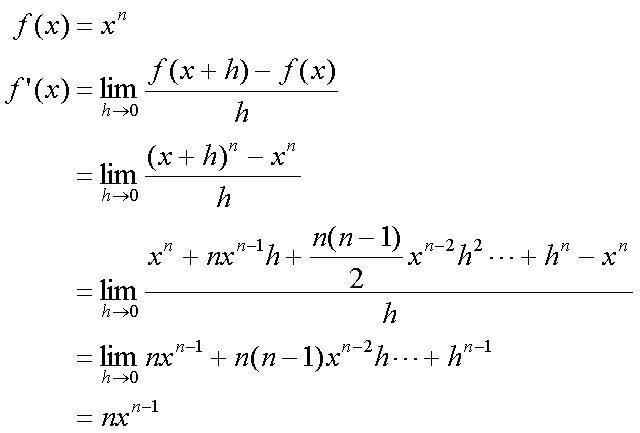

「えっと……真ん中のあたりはどうなってるの？」
「ああ、ｎ乗の展開なんだが……」

こういう三角を考えるんだ。

まず上から１を並べて、次の段は１と１を足して２、その次は１と２を足して３……

「えっと、つまりこういうこと？」

「そうそう。そういうことだ」

で、これはそのまま何乗で展開したってやつの係数になる。

分かってないみたいだな。
実際に展開してみな。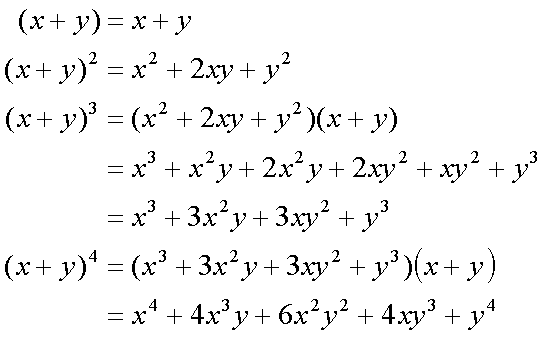

「えっと……あ、ほんとだ。全部係数に対応してるね」
「だろ？　開くときはこれが便利だから覚えておいたほうがいいかもな」

でまあ、この三角と、それぞれの次数が上がったり下がったりするのを考えると、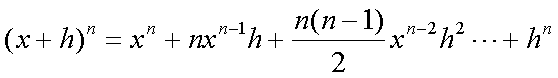

こう表せるってわけだ。
係数の数列については昔の人が一生懸命法則性を探した結果ってことでありがたく使わせてもらう。と。

話がだいぶそれたが、一般的にｘのｎ乗の微分ってのは、

こうなるってわけだ。
何乗ってのが前に出てきててるのがわかるよな。
ちなみに定数……この場合はxを含んでないものは、０になる。

んで、これでどうやって傾きを求めるのかと言うと、
次の関数で、ｘ＝２の点を調べてみるか。

まず微分してみな。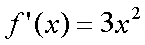

「こう？」
「OKだ。そしてそこに、傾きを求めたいｘを代入する」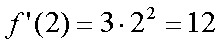

「……でいいの？」
「そうだ。ｘの3乗のグラフで、ｘ＝２のところは傾きが１２。実際グラフを書いてみると」

こんな感じになる。水色の線……つまり接線の傾きは１２ってわけだ。
接線の式を求めよって言われたら、
元の式からでf(2)=8だよな
つまり、（２，８）を通って、傾き１２の一次関数の式を書けばいい。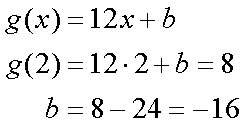

というわけで接線の方程式は、

「んー……ほんとだ。ｘが０のとき、－１６あたりだね」

でまあ、一般的には、接線の式はこう表される。

上ではa=2でおいたから、

こうなる。と。

あ、あと次の関係式は便利だから覚えておいた方がいいな。
ｆとｇはそれぞれ関数。ｃは定数な。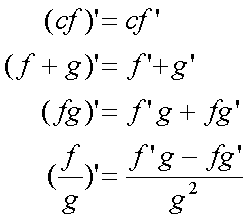

上の二つはさっき二次関数で試したとき分かったと思うが、aをc、ｘの２乗をｆとみればいい。微分したら２axだったよな。
ｘの２乗を微分すると、２ｘだから、それにaをかけたものだな。
あと、ｂｘを微分するとｂが残るし。

「えっと……ちょ、ちょっと待って」
「どうした？」
手を止めて稲穂のほうを見ると、なにやら頭を抱えていた。
ちょっと早かったか……
「もう１回。一番上の意味は、定数は微分に関係ないってことなの？」
「ああ、そういうことだ」
ｘを含まないものは微分に関係ないってことだな。
「で、えっと次のは……足し算された関数は、それぞれ微分するってことだよね」
「そういうことだ。引き算でも一緒な」
まあ、証明するまでもないな。大丈夫だろう。
「それで、次は……なに？」
「３番目は、積の微分と呼ばれている」
「掛け算だもんね」
その通り。関数ｆと関数ｇの掛け算だ。
「ああ。で、その微分の方法は、片方を微分したものに、片方そのままでかける。それを入れ替えたのを足す」
言葉にすると分かり辛いな……
まあ、式の通りだな。
「証明は？」
「してみるか？」
たまにはいいだろう。
「え、私！？」
やたら驚く稲穂。順を追えばできないことはないと思うが……
「ああ、まあやってみろ」
「うん。えっと……」

いきなり言われても……
とにかく、やってみようっと。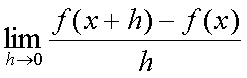

普通これだよね。
掛け算だから……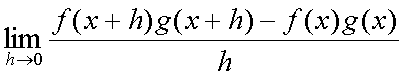

こうよね。で、次は……
次……
……詰まった。

「どうすればいいの？」
「うーん、何が欲しいのか考えろ。あと、何かを足しても、同じだけ引けば問題ない」

何かの暗号みたい……
と、気を取り直して、何が欲しいって、答えのあの公式よね……
やっぱりよく分かんないなあ。
何か足しても引けばいいってことは……何かを足すのよね。きっと。
……あ、もしかして。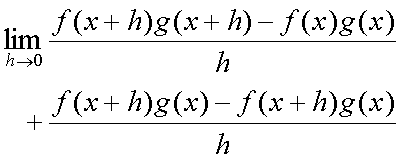

後ろのは……０よね。
達哉のほうを見てみると、小さく頷いてくれた。
えっと……ここからどうしよう。とりあえず、使えそうな形にまとめてみようかな。

微分できそうな形って……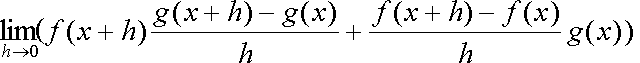

あ、それっぽい。
えっと、それぞれ微分した形に直すと、

あれ？

「おいおい。ちゃんとｈを０にしろよ」
苦笑いしている達哉。そっか。忘れてた。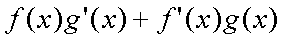

これで良し。っと。

「OKだな」
最後の証明はさらっと行くぞ。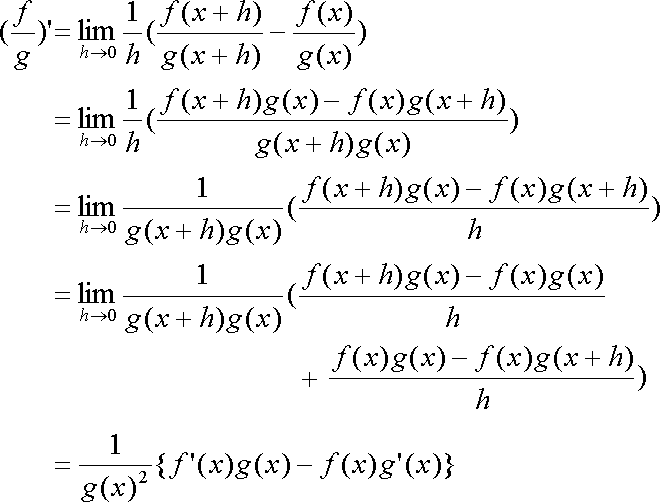

「すごいね……」
式が長すぎて２行になった……まあ分かってるみたいだからいいか。
「でもまあ、そんなにややこしくはないだろう？　通分して、分母入れ替えて……」
「必殺、足したもの引く」
別に必殺技でもないんだが。
まあ、便利な方法だわな。
「そう。それで例の形にそろえた」
ふんふんと指でなぞる稲穂。
その手がぴたっと止まる。
「あれ？　でも最後のはおかしくない？　足してるよ？」
公式と証明を交互に見比べている。
「よく見てみろ。ｇのｈだけずれてるのが後ろにあるだろ？」
「うん」
「－１でくくってみろ」
そうすれば前に来る。で、２項目はマイナスになる。
「えっと……ああ、ほんとだ。ちゃんとマイナスの微分になるね」
「そういうこと」
どうやら分かったらしい。
まあ、もう１行書いてもよかったかな……　

じゃ、例題。この２つを微分してみろ。

「まずは（１）から」
「うん」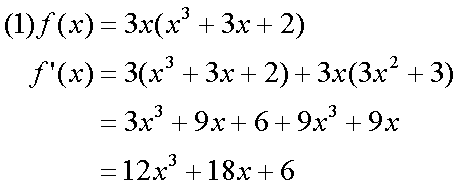

「これでいいの？」
ぱっと見……大丈夫そうだな。
「ご丁寧に使ったな。OKだ。でもこの程度なら普通に展開してからやったほうが早いかもな」
「せっかくやったのに、何でそんなこと言うの！」
ふくれる稲穂。
「悪い悪い。まあ、使い方の練習ってことで。はい、次」
「んー……微分するのは分子からだよね……」

「これでいい？」
「ん、多分間違ってないな」
まあ、ぱっと見なんだが。
「多分って何よぉ……」
またふくれる稲穂。
「ま、きっと合ってるさ」
そう責められてもなあ。
手順もあってるし、展開も間違ってなさそうだし……

「今日はこの辺でいいか」
やっぱしんどいな……微分まで来ると。
「結構頑張ったよね」
「ああ、そうだな」
まあ、数学やってるって気分にはなるが。
とはいえ、まだ微分の入り口だしなあ……
あと何回教えりゃいいんだか。テスト期間に引っかからなきゃいいが。
「これ使えたら、かっこいいの？」
「うーん、まあ、そうだな」
格好いい悪いは別にして、ここで引っかかってたら量子は夢だな。
いや、引っかかってもいいが。最終的に理解できれば。
「でも何乗ってしたやつを前に持ってきて、何乗を１減らすだけでしょ？」
「まあ、そうなんだが」
現時点ではな。
言葉にしてみると単純に思えるな。
だがそれが微分の基本だ。
「なんでみんな難しいって言うのかな」
余裕の稲穂。
公式見ながらやってるお前が言うなって。世間ではテストというものがあって……でもまあ、差し引いても理解力はあると思うが。
「多分他のことで頭がごっちゃになるんだろう。ｈの極限使うあの式なんて、覚えなくてもいいし」
「いいの？」
「ただの定義だからな。ｎ乗のを減らして……ってのを覚えてりゃ、それ知らなくても使えるだろ？」
証明は出来なくても、公式を覚えればいい。
数学なんて暗記科目だ。解き方さえ暗記できれば根本から理解する必要はない。
……ちょっと極端だが。
「うーん、それはそうだけど」
「定義式は余裕できてからでいいんだが、学校の授業だとどうしても順を追うからなあ……」
あのｈの極限とか全開ばりばりで展開される。
確かに、あれを黒板一面に書かれると、最初はげんなりするわな。
「結局覚えればいいことって……」
「ｘのｎ乗の微分と、最後に教えた関係式４つ」
それが出来ればまあ、基本はOKってことになる。
あとはそれぞれの関数について覚えるだけ……でもないが、それでなんとかなる。
「だけ？」
「だな」
ゆっくりやれば、理解できないことはないだろう。多分。
「ふーん……じゃあ大丈夫」
「ま、復習しとけな。この程度なら問題も適当に作れるし」
「そうだね。わかった」
稲穂が頷くのとほぼ同時に、玄関で物音がした。
「ただいまー。都君来てるの？」
部屋の主、佐倉さんだ。
「お邪魔してます」
「いらっしゃい。勉強中？」
「ううん。もう終わったよ。いいタイミング」
ほんと、いいタイミングだな。
「あ、そうなんだ」
冷蔵庫から麦茶を取り出して、佐倉さんが笑う。
その姿を見て思い出したけど、結構のどが渇いていた。
佐倉さんの勧めるままにコップを受け取って、３人仲良く麦茶を飲む。
夏だねえ……
一息ついたところで、佐倉さんが尋ねてきた。
「そういえば都君、今年の夏休みどうするの？」
「え？　どうするって……」
何についてどうなんだろう。
「いつもは実家に帰ってたよね。今年も帰るの？」
ああ、そのことか。
帰るつもりではいるけど……あ。
「えっと……」
そうか。
隣で幸せそうに麦茶を飲む稲穂を見る。こいつを置いていったら勉強教えられないもんなあ……
実家に帰るなら勉強教えられないもんなあ……
どうしようか。
「まだ、決まってません」
「そうなんだ」
草神は遠いからな……
ぐいっと麦茶を飲み干すと、稲穂が口を開いた。
「達哉、草神に帰るの？」
どう答えたもんか。
「あー、どうしようかと思ってな」
「帰るなら私も草神行こうかな」
意外な一言だった。
確かに、稲穂はここから動けないわけじゃないが。一応家出してるってことになってるし。
「行くって……あてはあるのか？」
まさか電車で通うわけにもいかないし。
「ほら、前に言ったじゃない」
「前？」
前、前……
頭の中を探ってみると、
「あー、もしかして……」
該当１件。
というか、稲穂と草神について話したことなんてそんなにないし。
「うん。神社。知り合いだから泊めてもらえるし」
そうか。そういう手段もあるか……
まあどうなるか分からんが。
「なんだ、稲穂ちゃんも泊まるとこあるんだね。それじゃあ私も帰ろっと」
佐倉さんが便乗してきた。
「稲穂ちゃん、草神で遊ぼう」
「あ、いいかもしれないね」
楽しそうなお二方。
なんだろう。俺の思考が遅いだけなのか、この二人の切り替えが早いだけなのか……
何となく取り残されたような気もするが、まあいい。
どうも夏休みは草神で勉強を教えることになるらしい。
一体どうなるのやら……

戻る