微分のお話２

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　微分のお話２

テスト範囲を示してくれる先生と、そうでない先生がいる。
量子の先生は後者だ。全く何も言わない。どこらへんを出すのやら……
「そういやさ、テスト期間中のバイトはどうするんだ？」
授業が終わったあと、米崎が聞いてきた。
「バイト？」
「かてきょ。やってなかったっけ？」
「ああ……」
バイトになるのか。
全くの無報酬なんだがな……
「引き続きかな」
稲穂のことだ。1週間我慢できないだろなあ。
ああ、でも適当に練習問題を出して自習させとくのもありか。
「高校のテストって、いつなわけ？」
変なことを聞いてくるやつだな。
「さあ……」
高校のテスト期間なんて、すっかり忘れた。
「さあって……お前、首かかってるんじゃないのか？」
「なんで？」
よっこらせと席を立つ。
学食行くか。
「いやほれ、成績下がってたらさ……」
「ああ、そういうことか」
普通の家庭教師ってのは成績が下がったらクビになる場合が多いのか。
「ま、大丈夫だろう」
「ずいぶん余裕だな……」
余裕も何も、そもそもテストなんかないんだから。
稲穂のやる気次第。
「科目なんだっけ」
「数学……」
うーん、物理にほとんど触ってないな。
まあ、積分までやってからでいいか。
「数学ね。理系？」
「まあ、そうだな」
理系だろうな……神社の娘で理系ってのもちょっと変な話だが。
「物理も教えるかもしれない」
いや、教えなきゃいけないんだが。
ってか、最終的な目標はそこだし。
「ほう。いいんじゃないのか？」
校舎から出る。
今日も暑い……
気持ち日陰を選びながら、学食へと向かう。
「数学バリバリ使って教えても大丈夫だろうか」
数学使っての物理に慣れさせたい。
「俺に聞かれてもな……例えば？」
「ん……ポテンシャルを積分で求めたり、ローレンツ力を外積で表したり」
他にもいろいろあるが。
まあ、高校数学を一通りやったあとなら、物理で使うのも難しくないだろう。
「ああ、そういうのか……まあ、いいんじゃないの？　でも高校で外積出ないとかいう話じゃなかったか」
「便利だから教えた」
覚えているかどうかはやや不安だが、稲穂ノートに書いてるから大丈夫だろう。
「それに、ポテンシャル求めるのって線積分とかいらないか？」
経路積分も教えるのか……
いつ物理やるんだよ。
「中心力なら距離だけの依存だし、何とかならないか？」
「それはそうだが……って、俺に言っても仕方ないって。その子がついていけるかどうかだな」
稲穂の顔を思い浮かべる。
あいつ集中してるときは耳に意識がいってないんだよな。それで、ちょっと物音がすると勝手に耳がぴくっと動く。客観的に見て集中してるのかしてないのか分からんのが特徴だ。
でもまあ、本人がそれに気付いてないってことは、集中してるんだろう。
「多分、ゆっくりやれば大丈夫だと思う」
何で稲穂がそこまでするのは分からんが、まあいけるだろう。
「……その子、頭いいんじゃないのか？」
「まあ、飲み込みは早いほうだと思う」
復習もしてるようだし。
単一の教科ってことも稲穂にとって良いんじゃないのかな。
「そら結構。楽なバイトでいいねえ」
「まあな……」
楽かと言われれば……あんまり楽でもないんだが。
まあ、ある程度生活が楽しくなったのは事実だからいいか。
そう思いながら、米崎と共にクーラーの効いた学食へと入って行った。

その日の夕方。
「達哉勉強してるんだ」
稲穂が勝手に入ってきた様子。
もうある程度は慣れたな……
「ああ、一応テスト前だからな」
さすがに何もしないのはやや不安だ。
「テストかあ……ちょっと憧れるかも」
えへへっと笑う稲穂。
「変なやつだな……」
「うーん、そうかな。でもやっぱり一度くらい受けてみたいよ」
ちょっと精神的にしんどいから、やめといたほうがいい。
とも言いたかったが、まあ力試ししたいってのもちょっとはある。
曖昧に笑ってみせると、俺はまた勉強に戻った。

晩ご飯のあとゆっくりしていると、稲穂がまた勝手に入ってきた。
まあ、インターホン鳴らされた方が驚くんだが。
「今日は何をするの？」
「微分」
今日も、だな。
「やったじゃない」
「あほか」
軽く頭をはたく。
「うわ、ひどい」
予想通り稲穂は口を尖らせる。
「1回ぐらいで微分が終わると思ってるのか」
「そりゃあ……終わったら受験生は苦労しないよね」
分かってるじゃないか。
「そういうことだ。さて……」
テーブルの上を片付ける。
よし、準備完了。
「今まで教えてきたが、関数にはいくつか種類があったよな」
正面に座る稲穂に言った。
「えっと……指数関数とか？」
「そう。あと、対数と三角があったな」
いまんとこそんなもんか。
「そうだね」
「その3つの微分について勉強する」
ちょっと複雑になるが、まあ勉強だ。

基本の式はこれだったよな。
別に覚えてなくてもいいが。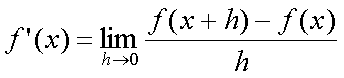

ま、早い話、これに代入していくだけだな。
f(x)=sinxとf(x)=cosxでやってみる。ああ、故あってｈは使えないのでｐを使う。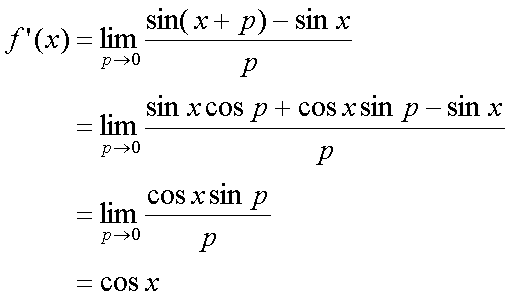

２番目から3番目は、sinxcosp→sinxcos0=sinxってことで、3項目のサインと打ち消しな。
ちなみに最後は、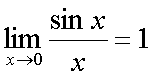

こういうのを使った
サインｘはｘが0に近付くと同じように0に近付くよな。
グラフにすると分かるが、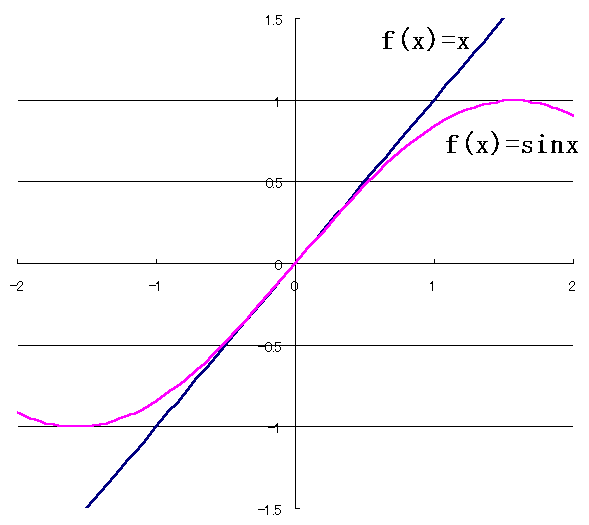

この通り、０付近ではほとんどsinx=xなんだ。
んで、上の式が成り立つと。
ああ、もちろんこれも使った。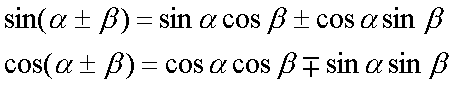

んで、次コサイン。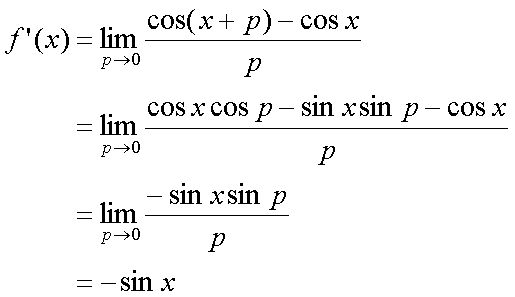

ま、今度はコサインが打ち消しあって、マイナスのサインが残ったわけだ。
これらの性質を使うと、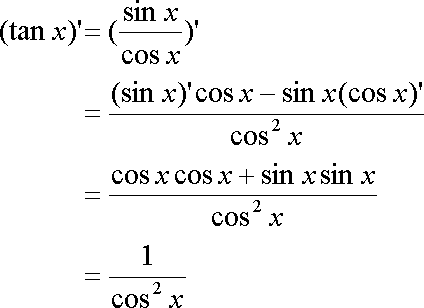

こうなる。タンジェントの微分も求められるってわけだ。

次は指数対数……といきたいとこだが、まず合成関数の微分を教える。

「合成関数？」
首をかしげる稲穂。
まあ、名前なんてどうでもいいんだが。
「ああ、今まではｘだけが変化してどうこうっていう話だったんだが、そんな単純な関数はそうそうない」
「どういうこと？」
「sin5xとか、cos(sinx)とかありえるってことだよ」
多くはまあ、ｘに係数がついてるだけだが。たまにそれ以上の凄い変な関数も出る。
「こ、コサインサインえっくす……？」
「コサインの中がサインで変化してるってことだな」
「う、うん……」
頭では分かっていても、想像しづらいだろうなあ……俺もそうだから。
でまあ、g(f(x))なんて表す。
今ので言うとだな、

こんな感じか。

「わ、わけわかんないよ……」
「ちょっとややこしかったか。つまりだ」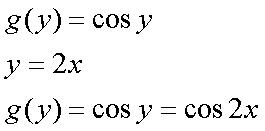

「これならどうだ？」
「う、うん……なんとなく分かる」

まあ、変数部分がただのxじゃなかったら、なんでも合成関数と見なせるわけだ。
でまあ、本題はこいつの微分なんだが、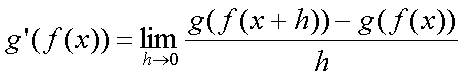

まあ、こうなるわな。
で、微分ってのは変数を微妙に動かして、それと同じので割る。
つまり、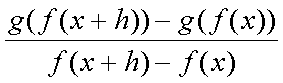

これが欲しいわけだな。
そこで、だ。

「必殺、足したものは引く！」
「……の分数版と言うべきものかな。分母分子に同じ物をかける。」
「あ、そっか。1を掛けても何も変わらないもんね」
「そういうこと」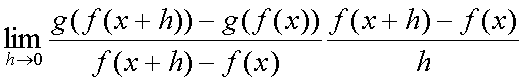

つまり……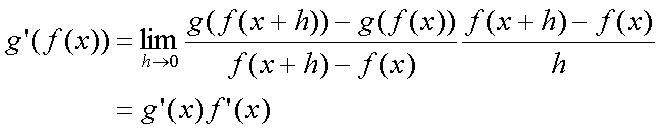

こうなる。
ｘでの微分かｙでの微分かはっきりしてないのが気になるな……ま、イメージだ。イメージ。要は微分したものの積になるってこった。
神経質な数学屋さんは何か言ってくるかもしれないが、まあ気にするな。

「えっとこれって……つまりどういうことなの？」
眉をしかめて稲穂が唸る。
まあ、ちょっとややこしいな……
「んー、さっきの例でいくと、sin5xってのがあったよな？」
「うん」
「それをだな……なんというか、sinyとy=5xで見る」
少しずつ教えればいいか……
「うんうん……」
「つまり……」

「やっぱり分かり辛いな……『'』がｘでの微分なのかｙでの微分なのか表してないからな……」
「あー……中のものも微分するんだ」
何となく分かってきたようだ。
「そう。そしてそれを掛ける」
「面倒だね……」
説明も難しいぞ。
「じゃあ、cos(sinx)でやってみろ」
「うん」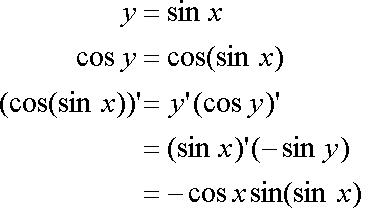

「……」
「ま、そんなとこだな」
えっと、サインの微分、コサインが出て、コサインがマイナスのサイン……ん、OKだな。
「なんか凄いことになるね……」
「まあ、気にするな。ｄを使った式で表すと、」

こっちの方がずっと分かりやすいな。
なにで微分するのかはっきりしてるし。
「あれ、これって、同じモノを掛ける作戦？」
「あー、まあそうだな。微分のこの記号は、分数と同じように扱える。数学屋さんは文句言うかもしれないが、今のとこそれでいい」
実際高校の数学の先生がぶつくさ言ってたからなあ……
確かに偏微分では話が違ってくるんだが。
まあいい。分かりにくかったから、2問とも書き直してみるか。

合ってるな。次は、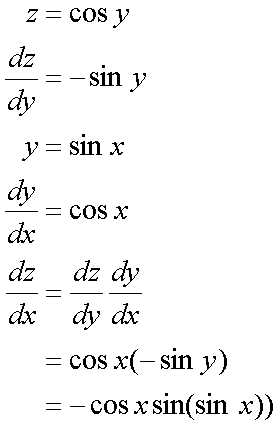

「うんうん。こっちの方が分かりやすいよ」
と、稲穂。
やっぱり最初からこっちにすりゃよかった……

さて、対数の微分だ。
底がaのlogxについて微分する。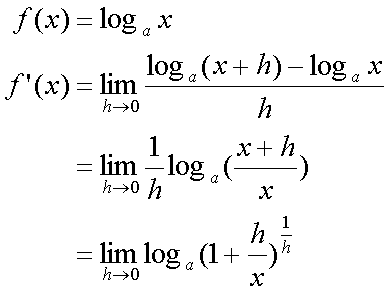

「ここまでは大丈夫か？」
「うん。対数の引き算は割り算にまとめられるんだよね」
稲穂ノートを開くことなく答える稲穂。
よしよし、ちゃんと覚えてたか。
「ん、じゃあ次。まず新しい数ｔを設定して……」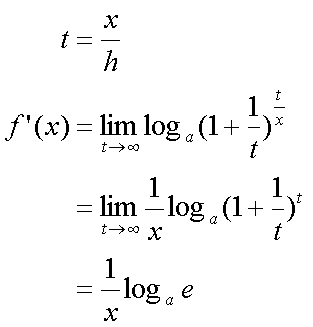

ｘ分の１を前に出してみると、どこかで見た形になる。
「eだ……」
「初めに気付いた人は天才だよな……」
誰だか知らないが、最初に気付くってことは並大抵じゃないよな……
「でまあ、分かると思うが底がeだった場合、答えは1/xになる」
つまり、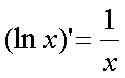

まあ結局底なんてほとんど……というかほぼ全部eだから、これを覚えりゃそれでいい。

次、指数関数。
さっき微分の記号は分数みたいに扱っていいって言ったよな。
だから、

こうできるわけだ。
eのｘ乗の場合、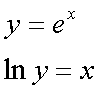

両辺の対数を取って、こう置くことができる。すると……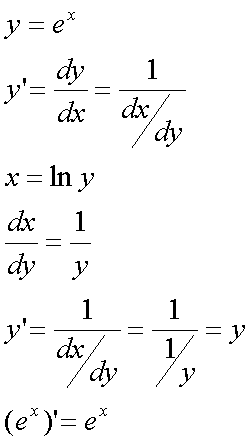

「えっと……変わってない？」
「そういう関数だからな。eは便利だ」
eのｘ乗は、微分してもeのｘ乗。
ああ……なんて変な、そして素晴らしい関数なんだろう。
「これってeのｘ乗っていうのにしか使えないの？」
「ああ……」
他の指数についてもやらなきゃな。

一般的なのは、
aのｘ乗だな。
まずは変形から。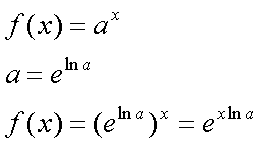

「ちょっと待って。2段目なに？」
「ああ、これか……両辺の対数を取ればすぐ分かる」

「ほんとだ……えっと、じゃあ続き」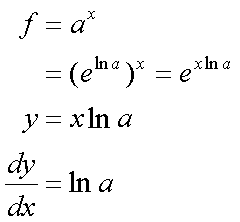

ここまでは大丈夫だな。
さっきの変形をｆに代入して、ｙを置いてｘで微分した。
次はｆをｙで微分して……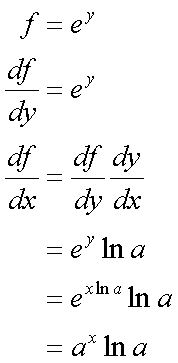

掛け算すれば終わり。と。
「最後のはえっと……最初のだね」
「分かりにくいが、まあそうだ」

よし、まとめ。
覚えるべきはこれだけな。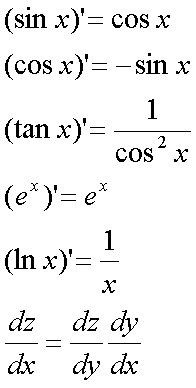

「頑張った割に、覚えることは少ないね」
「まあ、証明が面倒なだけだからな」
やらなくてもいいかなあ……証明。
でもずいぶん味気なくなるしなあ。
「んじゃあ、最後に練習問題やってみるか」
「うん」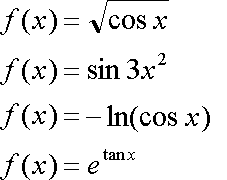

この4つかあ……
ゆっくりやれば何とかなるわよね。きっと。

えっと、まずｙを置いて、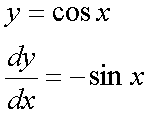

ｙのｘ微分。
次は、ｆのｙ微分を導いて……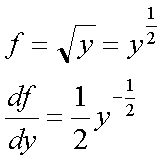

こうかな？
あ、達哉が頷いてる。
よーし、じゃあ仕上げにこの2つを掛けて……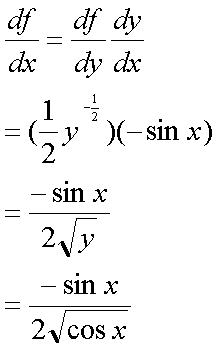

終わり……かな？
うん、大丈夫そう。
ちょっと時間かかっちゃったな……
あ、でも次のは簡単そう。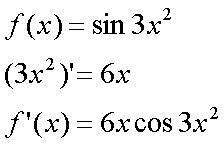

あはは、達哉ちょっと驚いてる。
結局中身が微分されながら外に出てくるだけなんだよね。
うん、何となく分かってきた。
じゃあ、次。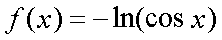

えっと……ｙを置いた方がいいかな。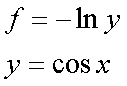

こうよね。
で、それぞれ微分してみたら……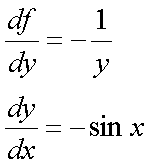

こうかな。
稲穂ノートで確認……あ、大丈夫そう。
あとは掛け算すればいいから、

うわ、タンジェントが出てきた。
初めの形からは想像できないや……
えっと、じゃあ最後の問題。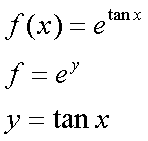

こうよね。
あとは微分して掛け算……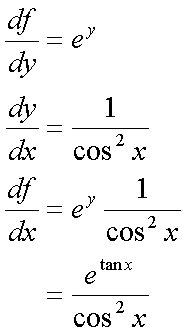

……大丈夫そう？
うん。達哉が頷いてるからおっけー。

「お疲れ。よくできたな」
「うん、ちょっと稲穂ノート見たけどね」
ゆっくりでも出来ればいいさ。
2問目はさっさと解けたしな。
「まあいいさ。お前は受験生じゃないんだし」
「そうだね……」
それにしても飲み込みが早いな……
ちょっと前まで中学生レベルだったとは思えん。
「達哉はこれ見ないでやったの？」
「当たり前だろ」
見れるか。そんなもん。
だからテスト前には必死に勉強してたんだし。
「すごいね……」
「いや、演習やってたからな……」
高校時代の先生は宿題とか称して問題どかばかやらせてたんだが、結果的にそれで力になってるんだなあ。
「繰り返し使ってりゃ、嫌でも覚えるさ」
なんにしてもそうだろう。
実際使わない歴史とかだいぶ忘れてるし。
あ、覚えるといえば。
「そうだ、自転車乗る練習はいつにする？」
草神でもいいんだが、知り合いに出会う確率を考えると、こっちの方がいいな……
「うーん、私はいつでもいいよ。達哉テストあるでしょ？」
うお、稲穂が気遣ってくれるとは……
「助かる」
「うん。じゃあ達哉のテストが終わってからね」
嬉しそうに笑う稲穂。
どうにも退屈しなくてすみそうだ。
「勉強の方はギリギリまでばしばし教えてやるからな」
テスト前までには積分……と思ってたがちょっと無理そうだな。
積分は草神に戻ってからだ。
「あはは、お手柔らかにー」
ギリギリ……か。　
テストまであと1週間。教えられてあと１回ってとこだな。
さて、勉強勉強……
稲穂が帰ったあと、俺は机に向かった。

戻る