微分のお話３

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　微分のお話３

今日もやっと授業が終わった。といってもまだ昼過ぎなんだが。
テスト前だからってペースが変わるわけじゃないが、少し疲れたな……
学校近くのスーパーで買い物を済ませ、アパートへと足を向ける。
「ねえねえ、知ってる？」
前方から賑やかな声が聞こえる。近所の中学校の生徒だろう。
そういえば下校時間って、このくらいの時間だっけか……と、そこまで考えたところで短縮授業の存在を思い出す。
「あの家にね、なんていうの？　猫耳？　つけてる女の子が住んでるんだって」
！？
彼女の指差す先に、うちのアパートがあった。
ま、まさか……
「なにそれ。コスプレかなにか？」
「かもね。たまに見かけるらしいよ」
あの部屋だったかなと指差す先は、佐倉さんの部屋……確定した。
「へえ……変な人もいるもんね」
「ねえ」
歩くスピードを落とし、彼女らが見えなくなってからアパートへ駆け込んだ。

自分の部屋に荷物を放り込むと、すぐさま隣の部屋のドアを開ける。ノックは一瞬。
「稲穂！」
うちわを持って寝転がっていた。もちろん、耳と尻尾は出しっぱなしだ。
「へ、どうしたの？」
ふいっと上体を起こすと、稲穂は不思議そうな顔でこちらを見た。

「そうなんだ」
今聞いてきたことを話すと、稲穂は一言そう言った。
「そうなんだじゃないだろ……どうすんだよ」
のん気な奴だな、おい。
「うん、気をつけるよ」
「ほんとかよ……」
どうにも不安だ……
まあ大丈夫だとは思うんだが……変な噂が広がっても困る。
はぁ……とため息をつくと同時に、ドアの開く音がした。
「ただいまー、あ、都君」
「お帰りなさい、佐倉さん。ちょっと聞いてくださいよ……」
と、佐倉さんに言おうとしたその時、
「見て見て、これどうかな？」
佐倉さんがかばんから取り出したそれは、いわゆる猫耳……
「佐倉さん……」
どうしてこう、この人は……
「稲穂ちゃんとお揃い」
装着。ちょっと可愛かったりするから卑怯だ。
「ほんとだー。ちょっと違うけど」
はしゃぐ二人。取り残される俺。
なんだ……俺が間違ってるのか？
「そんなの、どっから仕入れて来るんですか……」
「あ、今度都君の分も」
「いりません！」

……いろいろあったが、とりあえず自分の部屋に戻って勉強を始める。
「今日のテーマは偏微分だ」
「へ、変？」
「偏った偏。変なのは耳だけで充分だ」
「わ、酷いこと言ってる」
まったく、佐倉さんといい、稲穂といい……

数学の問題ではともかく、物理ではいろんな変数が使われる。
温度然り、体積然り……まあそれは熱力学で説明するが。
……いつになるんだろうな。
ともかく、変数は1個じゃない。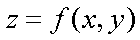

微分の考えを2変数に拡張してみるぞ。
書きづらいんだが、グラフはまあこんなのになる。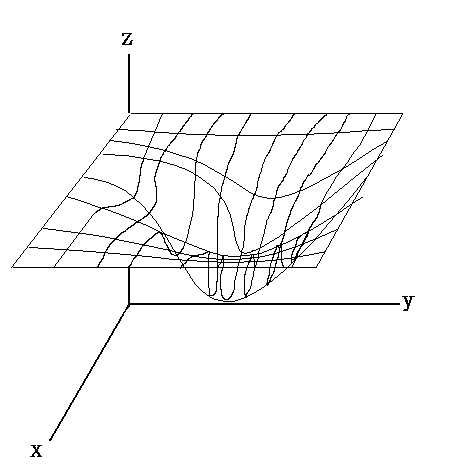

気持ちは分かってくれ。３次元だ。
これじゃあ微分の本来の目的……傾きを調べるってやつな。それがどの方向での傾きなのか決まらないよな。
例えば山の中腹にいるとする。頂上向かって前後はもちろん坂だよな。でも、左右はそんなに傾きがない。階段ならともかくハイキングコースは緩やかな傾斜の左右を選ぶよな。
今度ハイキングでも行こうか。

「うんうん。行こう行こう」
「いつになるか分からないけどな」
夏休みに行ってもいいんだが。
「草神でもいいんじゃない？　割と近いし」
どうも稲穂も同じ考えだったらしい。確かに、草神は山が割と近い。
「ああ、そうだな」
佐倉さんも誘って行ってみるか……

……と、話はそれたが、えっと、なんだっけ。
ああ、つまりだ。傾きを調べるのにだな、軸と平行にぶった切るわけだ。
こんな感じ。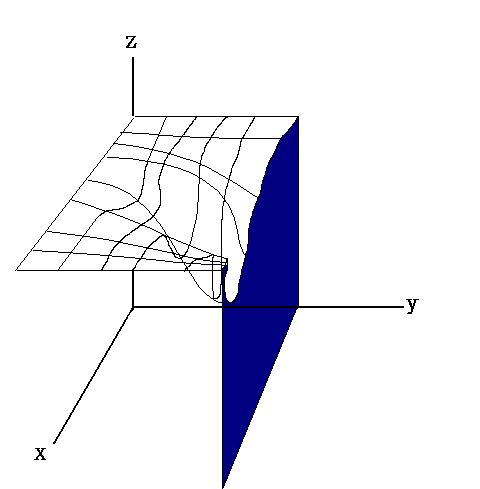

二次元のグラフに直してみると、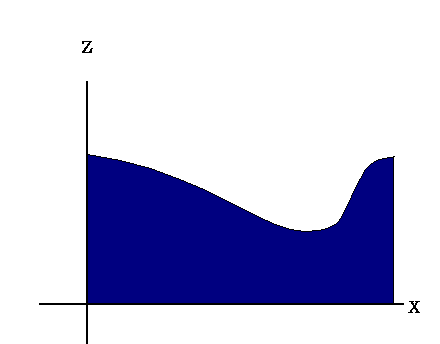

まあ、こんな感じか。気持ちだけ分かってくれ。
で、この二次元に直したグラフで傾きを見るわけだな。ｚ（というかf(x,y）だな）をｘで微分するわけだ。
これはｙ一定……変化を止めているわけだよな。ｘだけで微分しているわけだ。
でまあ、それをこう表す。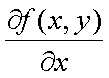

これが偏微分。この変な記号はラウンドとか呼ぶが、まあｘの偏微分でいいだろう。
具体的な計算方法は、ｙが動かないんだから、ｙを定数と見てやればいい。

「定数……」
「じゃ、練習問題。やってみな」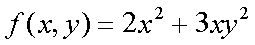

「ｘの偏微分から」
「えっと……」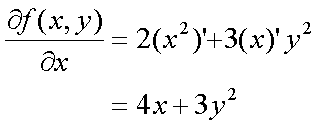

「これでいいの？」
「ああ。つぎ、ｙでの偏微分」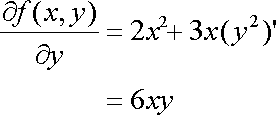

「ｙを含んでないところは定数だから消えちゃうよね」
「ああ、それでOKだ」

「じゃあ次、やってみろ」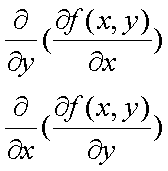

「えっと……今の答えをもう１つの変数で偏微分するんだね」
「ああ、そうだ」
ちゃんと分かってるな。よしよし。
「えっと……」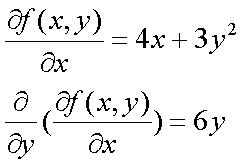

「ｙがないところは消えちゃって、後ろの部分だけ微分だよね」
「よしOK。じゃあ次」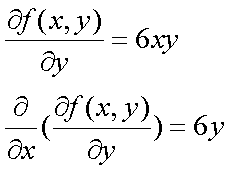

「ｘで微分だから……あれ、一緒になった」
少し驚く稲穂。
「そうだ。何が言いたいかというとだな、順番は関係ないぞと」
「うん、わかった」

さて、全微分というものがある。
まず変数1個のときから考える。
変数f(x)がちょこっと動くってのは、ｘがちょこっと動いて、その傾きをかけたものに等しい。つまり、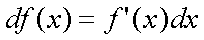

グラフを書くとこんな感じな。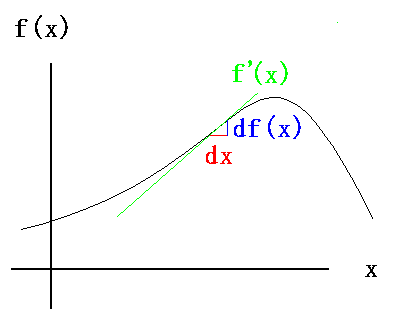

黄緑は傾きがf'(x)ってことな。
「うんうん。そうだね」

でまあ、これは……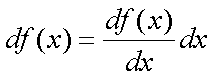

こうだわな。まあ、そもそもdf/dx=f'(x)だしな。

でまあ、これを2変数のときに当てはめてみる。
2変数のz(x,y)がちょこっと動くってのは、ｘもｙもちょこっと動いてる。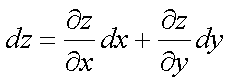

「あー、ここで偏微分の出番なんだね」
「まあそういうことだな」
別にこれだけじゃないんだが。まあいいか。
「でまあこいつがだな、全微分なんて呼ばれる」
「偏微分と全微分……ややこしいなあ」
ややこしいって……響きが似てるだけじゃないか。
「でもやってることは全然違うだろ？」
「うん。まあね」

でだ。
偏微分は分数と同じように扱えないときもあるって言ったよな。自信ないけど。
それを証明する。
いきなりだがｚの動きを止める。つまり、dz=0だ。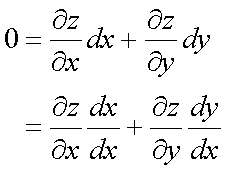

で、dxで割った。当然１項目の後ろは１だから、

で、さっきも言ったがｚを固定してるってことはだ。ｙの関数に直したときのｘの微分は偏微分と同じだ。ｙイコールの式にして、ｚを定数で扱うんだからな。
というわけで続き。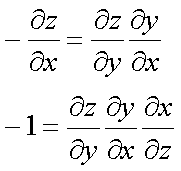

「ほんとだ。マイナス１になるんだね」
「ってことで、微妙に扱いが異なる。具体的には熱力学を使うときにならないと説明できないんだが、まあ稲穂ノートに書いておけ」
「うん。でも、最後って分数と同じように移項してない？」
「ああ、それは大丈夫」
全微分の式で、ｙを固定する。dy=0だ。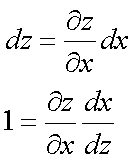

で、dy=0ってことは、ｙ固定。定数として扱うから、偏微分と同じ。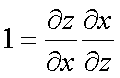

「ふーん、これだけなら同じように使っていいんだ」
「ああ、重要なのは複数絡んだときの処理な」

さて、まあずっと微分をやってきたが、これで何がわかるかってのを教える。
微分したら傾きが出るってのは教えたよな。
でもまあこの傾きなんだが、正ならグラフは右上がり、負なら右下がりだよな。で、０なら平行。
ま、口で言うより実際やって見るか。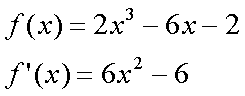

微分するとこうなるわけだ。
微分して０になるところは……

「１だね」
「プラスマイナスな」

表にするとこうなる。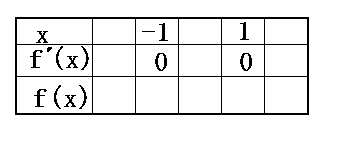

適当に間を埋める。
f'(0)＝-2
ってことで、－１と１の間はマイナス。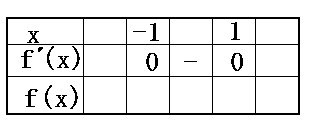

あとｘが１より大きいときは微分したら正。－1より小さくても、微分したら正。
「えっと……うん、そうだね。」
ってことで埋める。でまあ、微分したものが正か負かで、上がってるのか下がってるのか分かるから……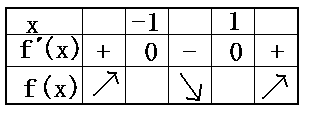

ということから、グラフの大体の形が分かる。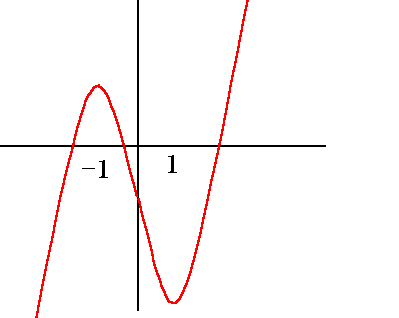

こんな感じな。かなり適当だが。
でまあ、微分したら０になるところを極値というんだ。
この場合、ｘ＝－1で極大値をとる。
ｘ＝１で極小値を取る。

「極値……」
「まあ深く考えなくてもいい。ただ、グラフの増減が分かるってだけだ」

でまあ、より詳しく知るためには、もう1度微分する。2回目だから２回微分と呼ばれる。２階とも書いたりするが、別にどっちでもいい。
まあ、簡単に言えば、減る勢い、増える勢いがわかるわけだ。
増え方、減り方はこの4種類な。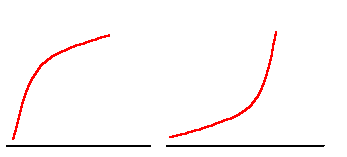

増え方が鈍くなっていく左と、増え方がどんどん酷くなっていく右。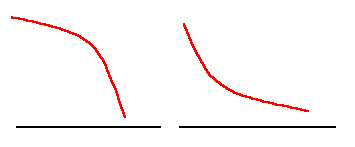

減り方がどんどん酷くなっていく左と、鈍くなっていく右。
それぞれ左側が２階微分負。右側が２階微分正。
正なんだから減りが弱く、増えが酷くなってるのは分かるな。
負だったらもちろん減りが酷くなって、増え方は鈍くなる。

さっきのグラフで考えると、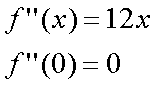

ってことで、０が切り替わる地点ってわけだ。
正は０の右……ってことは、減りが弱くなって、増えが酷いだろ？
逆に０の左は負だから、増え方が弱くなってきて、減り方が酷い。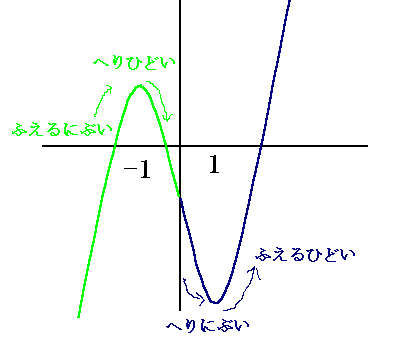

「……この点々2個は、2回微分？」
「あれ、教えてなかったか」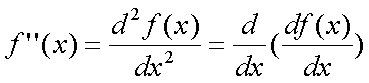

「こんな感じな。２乗みたいに書く」
「でも実際は、１回微分して、それをもう１回微分するんだね」
まあ単純だな。

じゃあ練習してみるか。
次の２つの関数の２階微分を求めてみろ。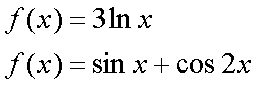

適当に書いてみる。まあ、できるだろう。

「じゃあ最初からね……えっと、３はおいといて、ログの微分は……」
稲穂ノートをぱらぱらとめくる。まだはっきり覚えていないらしい。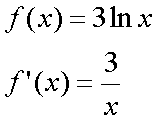

「こう？」
「ん、次」
「うん。ｘ分の１は、ｘのマイナス１乗だから……」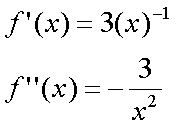

「そうだな」
少し微分にも慣れてきたかな。
次の問題に取り掛かる稲穂。
三角はノートなしでも大丈夫のようだ。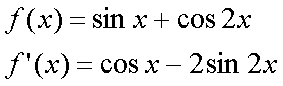

「こうだよね」
うん、大丈夫そうだ。
「ちゃんと忘れてないな」
「え？」
「２が前に出るってこと」
「うん。２ｘを微分したやつだよね……それから」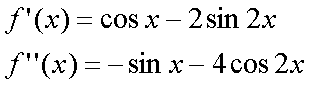

「こうかな」
「ん、OKだ。だいぶ慣れてきたか」
「うん」

じゃあ、1問目についてのみ、増減を求めてみろ。

「えっと……」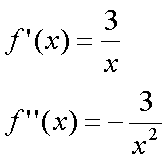

「こうだから……」
「ああ、ちなみにlnだから、ｘは０以下をとれないぞ」
「うん……えっと」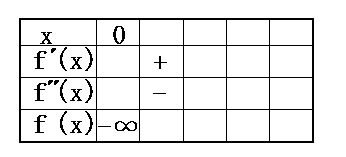

「って、じゃあずっと同じような増え方じゃない」
「だな」
まあ、lnxのグラフを思い出せばすぐわかると思うんだが。
ちなみにいつかは増えるのが止まりそうにも見えるが、ｘ無限大のときはlnxも無限に飛ぶ。

今日はここまで。
自分で適当な関数作って増減調べる練習してもいいかもな。

「さて」
夏は日が長い。
日が沈むまであと1時間はあるな。
「うん？」
「自転車乗る練習するか」
「今から？」
稲穂ノートをしまいこむ。
そろそろ新しいノートが必要かもな……
「まだ明るいだろ」
「んー、わかった」
隣の部屋へ戻って行く稲穂。
玄関脇に置いてあった自転車の鍵をポケットにしまう。
学校へは歩いて通ってるから、自転車乗るのは結構久しぶりだな……
靴を履いて外へ出る。
昼に比べれば日差しはマシになったとはいえ、やっぱり暑い。緩やかに吹く風が、なんとも心地いい。
「都君」
「あ、佐倉さん」
と、稲穂。
「自転車の練習だよね。どこでするの？」
「うーん、前の道でもいいんですけど」
そんなに交通量もないし。
「ええっ、嫌だ。恥ずかしい」
いきなり文句が出た。
「他は……神社」
「もっとダメ！」
わがままな奴だな……
「都君、実ヶ池公園はどうかな」
悩む俺に、佐倉さんがこう聞いてきた。
「実ヶ池公園……」
って、線路はさんで向こう側じゃなかったっけか。
ちょっと遠くないか？
「少し距離があるけど、思いつくのってそこしかないよ」
「そうですね」
確かにそうだな……
「じゃ、けってーい！」
はしゃぐ稲穂。声が大きいって。
「まあ、とりあえず行きますか」
「うん」
もちろんそこまでは自転車。なのだが……

「で」
「うん？」
首をかしげる稲穂。
「何で俺の自転車の後ろに乗ってるんだ。お前は」
当然の如く俺の自転車の後ろに座る稲穂。
最近の自転車にしては珍しく荷台がついているため、座りやすい。引っ越してきたてのときは荷物を運ぶのに活躍したものだが……
「だって、ゆかりちゃん女の子だし」
それは理解できる。だが、
「歩け」
「えー、やだよ」
二人乗りなんて怖くてできるか。
万が一事故ったらどうするんだ。
「二人乗りは違反だ」
「細かいなあ、達哉」
そういう問題か。
……そりゃあ、信号無視したことがないかと言われれば、あるんだが。
「第一、重いだろ」
「うわ、すっごく失礼だよ、それ！」
実際、普通の荷物よりは重いだろ。
と、外野から平和そうな声が聞こえてきた。
「二人ともー、早くしないと日が暮れちゃうよー？」
佐倉さんが自転車に乗って、前の道路でくるくる回っている。
言っちゃ悪いが、ちょっと間抜けだ。
……まあ、言ってることはもっともなんだけど。
「ほらほら」
べしべし背中を叩く稲穂。
「はぁ……まったく」
そうつぶやくと、諦めてペダルを踏む。
少しずつ周りの空気が流れ始める。多少だが涼しい。
そして、俺の背中に体を預ける稲穂は、思っていたよりも軽かった。

戻る