エネルギーのお話

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　エネルギーのお話

「あー、えっと、草神か」
瀬良を出て、
「おはよー、達哉」
志乃上で稲穂を拾い、
「早く切符買って入ってこい」
草神で降りると、
「あぢー……」
バスに乗り、
「あ、次だ。西水台橋」
到着したのは、
「ここかあ……」
佐倉さんち。

インターホンを押すと、扉が開いた。
ひょいと顔を出したのは、どことなく佐倉さんに似ている女の子。天然栗毛の髪は佐倉さんより短く、肩の辺りまでの長さ。
「はーい……えっと、どちら様ですか？」
「えっと、家庭教師というか、なんというか」
てっきり佐倉さんが出てくると思ってた俺は、答えに詰まる。
我ながらえらく挙動不審だったが、どうやらそれだけで通じた様子。
「あ、都さんでしたっけ」
「そうです、それ。えっと、志津子さんですか？」
「ええ、私が佐倉志津子です。姉がいつもお世話になってるそうで」
そう言って頭を下げる志津子さん。
「いえいえ、とんでもないです」
お世話になってるのはむしろこっち……
「私が一番お世話になってるよね」
と、笑う稲穂。大正解だ。
「だな……と、こっちは」
「稲穂さんでしたよね。よろしくお願いします」
稲穂のことも話が行っている様子。
説明が省けて楽だ。一方、その稲穂。
「あ、よ、よろしくお願いします……」
若干の人見知り。
ヘアバンドは外さないようにしないとな。

勉強する場所がないと佐倉さんに言ったところ、気前よく提供された佐倉家。だが条件として、佐倉さんの妹、志津子さんの家庭教師もついでにやってくれとのこと。
佐倉家は２階建てのごく普通の一軒屋。
俺たちが通されたのは、１階のダイニングっぽいところ。
「ちょっと待っててくださいね。姉さんはちょっと出かけてて」
そう言って志津子さんはどこかに行ってしまった。
とたとたと廊下を走る音が聞こえる。
「佐倉さんの家かあ……」
「ちょっと手狭だね」
「そういうことは言うもんじゃないぞ」
とはいえ、確かに狭い感じがする。なんというか、物が多い。
きょろきょろと辺りを見ているうちに、
「はい、お待たせしました。よろしくお願いします」
勉強道具を持った志津子さんが現れた。
「こちらこそ……」
ちょっと緊張するな。稲穂と違って無責任に教えられないし。
３人四角い机に座る。
さて、授業開始だ。

えー、今日のテーマはエネルギーについて。
エネルギーの単位は知ってるかな？

「カロリーですか？」
即答の志津子さん。だが半分外れ。
「うん、まあ、それもあるんだけどね」

物理ではカロリーは使わない。主に「ジュール」を使う。
これについてはまあ深く突っ込まないけど、じゃあカロリーの定義は知ってる？
そう。1ccの水の温度を、１℃上げるエネルギーだよね。それが1cal。
でまあ、これは化学でよく使う単位なんだ。物理ではあまり水を温めない。水を温めるより、物を動かす方が多いんだ。
だから、エネルギーの単位にJ（ジュール）を使う。で、それは「物体をFの力で距離ｒ動かすエネルギー」と定義される。力が物体にした「仕事」と言われるな。まあ、呼び方はどうでもいいが。
１Nで１ｍ動かすのが１Jのエネルギーなんだ。
式で表すとこう。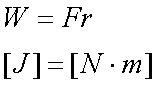

じゃあ稲穂、Jをｍ、kg、sで表してみろ。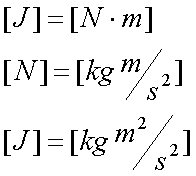

うん、OKだ。
でまあ、１次元のときはこれでいいんだが、実際はこうも行かなくなってくる。
というのもだな、この式は「力が働く方向と全く同じ方に物体が動く」と考えて定義されてるんだ。こんな風に。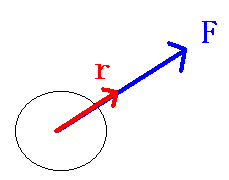

だけど……まあ例えば、物を引きずって持っていくときはこうなってるよな。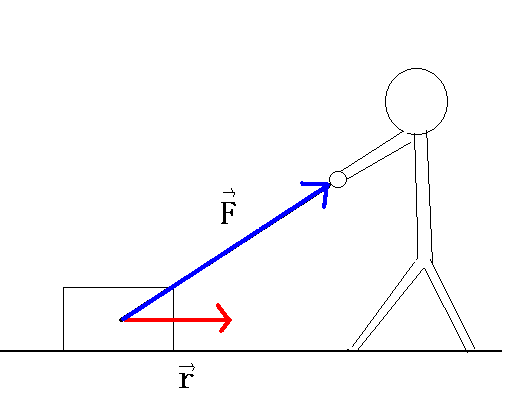

つまり、力がかかってる方向と、物体が動いてる方向が違ってるわけだ。

「うわ、細い足」
「うるさい」

……気を取り直して。
でまあ、これを解決した式がこれ。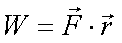

内積を取るわけだ。
証明……とまではいえないが、さっきの図で考える。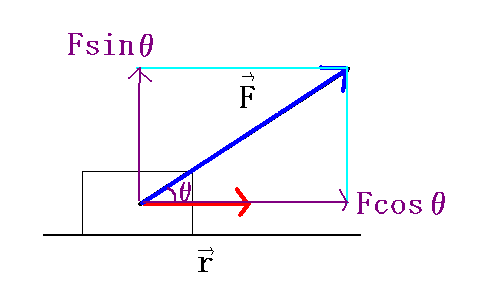

力を分解してみたわけだ。
この場合、動いている方向と同じ方向にかかる力は、Fcosθになるよな。
内積の定義も同じってわけだ。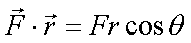

「はーい、質問」
「どうぞ」
突然の質問に、やや緊張。
「重いものも軽いものも一緒なんですか？」
「というと？」
「１Nの力で１ｍ動かすんですよね。重い方が動かすのは大変そうに思えるんですが。それでも同じ１Ｊなんですか？」
あー、そういうことか。
「んー、そうだね。その答えはジュールの単位に入ってるんだけど……」

じゃ、この辺で単位の話でもしておくか。
一定の物理量を考えようか。ある速度ｖについて。
ｖの単位はこうなってる。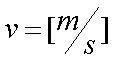

ｖがある数だった場合……そうだな。ここでは１m/sとでも置こうか。
距離が２ｍだったらｓはいくらかかる？

「２秒ですよね」
「正解」
即答の志津子さん。
ま、そら分かるわな。
「じゃあ、１０ｍのときは？」
「１０秒。達哉、バカにしてる？」
とは稲穂。言うと思った。

まあまあ。バカにしてるわけじゃないから。
話の続き。
今度は運動量を考えてみようか。
単位はこう。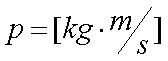

質量×速度だからまあこうなるわな。
でまあ、これも……うん、２kgm/sとでも置こう。
速度が２m/sだったら、質量は？

「１……ですよね」
「そう、１kg。じゃあ、速度が４m/sのときは？」
稲穂に聞いてみる。
「４？　えっと……２分の１？」
「だな。あえて小数で表すと、0.5kg」
と、そこで志津子さんがうなずいた。
「ああ、なんとなく分かってきました。結局、別のところでバランスが取られるわけですよね」
「うん、まあそういうこと」
言いたいことは伝わったらしい。
「Jの単位はkg･m^2/s^2だから、kgが大きいときは、m^2/s^2が小さくなる」
「なるほどね。力がないぶんゆっくり動かすんだ」
稲穂も納得した様子。
「イメージとしてはそうなるかな」
ま、大したことじゃないけど良かった良かった。
「実際は摩擦があるから、やっぱり重いものの方がしんどいんだけどね。特に断りがない場合は摩擦無しのつるつるすべるところで動かしてるって考えてくれ」

でまあ、ある力をかけて物体をずるずる動かすわけだが。
１次元で考えてみるが、つまりはこういうグラフだよな。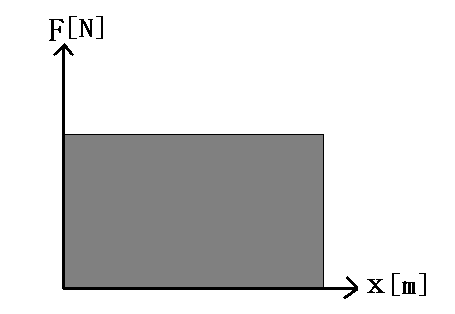

一定の力である距離を動かしている様子だ。

「えっと、この面積が仕事？」
お。稲穂が気付いた。
「そうなるな。縦の力に横の距離を掛けたら例の単位が出るし」
Nにｍを掛けるとJの単位。これはさっきやった通り。
「ということは、だ」
「？」
分からない。といった様子の志津子さん。
対して稲穂は、
「積分！」
「正解」
ばっちり分かっていた。

距離をｘとして、こんな積分で表されるわけだ。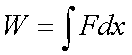

これが後々重要になってくるんだが、ひとまず置いておく。
面積→積分の発想ができるとは、稲穂もなかなかやるな。

さて、エネルギーっていっても、いくつか種類がある。
重要なものとして、運動エネルギーと位置エネルギーがある。
運動エネルギーの定義としてはこんな感じ。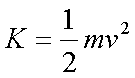

質量に速度の二乗を掛けたものを２で割ると出る。
位置エネルギーは、まあいろいろ。
単位を確認すると、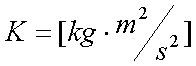

この通り。さっきと同じだよな。
運動エネルギーについてはあまり教えることはない。
重くてスピード出てるものはそれなりにエネルギー持ってるってことだよな。

で、位置エネルギー。これはまあ、ポテンシャルエネルギーとも言うな。
高校物理では前者。大学になると後者の呼び方をよく使う。
これは何かと言うと……うーん、説明が難しいな。
例えば稲穂。こう、ノートを持ち上げているとするだろ？　手を放すとどうなる？
そう。下に落ちるよな。
落ちるってことは、速度を得てる。つまり、上に持ち上げた状態っていうのは、潜在的にエネルギーを持ってるってことなんだ。
このエネルギーはどこから来てるのかっていうと、手で持ち上げるこの動作。これがノートにエネルギーを与えてるわけだな。

で、物体には重力がかかってる。
F=maだから、そう。質量をｍとして、mgの力。
で、これに逆らって上にあげてるわけだ。つまり、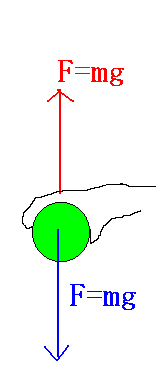

こんな力のかかり方。これは白蛇じゃなくて手な。気持ちは分かってくれ。
でまあ、高さｈまで上げたとすると、仕事はもちろん、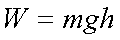

になる。
ちなみにこれはゆっくり持ち上げた場合な。
ｍｇ以上の力で早く上げてもいいんだが、その分は運動エネルギーになってしまう。まあ、今は深く考えなくていいや。

「えっと……うんと……」
「ううー……」
唸る二人。やっぱちょっとつかみ辛いか。
「ちょっと難しかったか」
「うん。分かり辛い」
はっきり言ってくれるなあ。
でもまあ、それが稲穂のいいところでもあるが。

じゃあちょっと説明を変えてみるか。
全ての物体にとって、エネルギーが低いところが安定となる。
まずこれを覚えてくれ。根本だから。
エネルギーが高いってことは即ち不安定なんだ。物体は基本的にこれを嫌うと思っていい。
例えば、さっき言ったとおり、高いところはエネルギーが高い。物体は全部高所恐怖症だと思えばいい。１００メートルのビルの上より、地上の方が安心できるってわけだ。

「うんうん。それなら分かります。私ちょっと高所恐怖症なんで……」
と、志津子さん。まずこれを分かってもらわないとな。
「それで……えっと、物体は低いところの方がいいんだね」
「そういうこと」

で、そうなると地上からビルの上にあげるには、物体を説得しなきゃならない。というか、基本的に物体は上に行くのを嫌がるわけだ。
そこで力をかけて仕事をし、持っていかなきゃならない。質量が大きいほど、腰が重いわけだな。
つまり、重い荷物を持ち上げるのは、相応のエネルギーが必要で大変だってわけだ。
そして手を放すと、物体はすぐにでも下に落ちたがる。エネルギーが低いからそっちのほうに向かおうと必死なわけだ。

「だからこいつは」
消しゴムをつまみ上げると、
「ここよりも下にいる方がいい。ってか、安定」
ぽとりと机に落とした。
「だから落ちるわけだ」

概念は以上こんな感じ。
で、高さｈでの位置エネルギーの式はこんな形になる。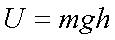

さっきの通りな。
で、これはつまりmgの力でｈまで上げたってことだから、この積分。

というわけだ。

「うん、なんとなくわかった……かな」
「私もなんとか」

うん。でまあ、この話にはまだ続きがあって……
エネルギーってのは保存する法則がある。
どういうことかというと、まあ位置エネルギーと運動エネルギーの和は不変ってことだ。
例えば、ｈまで上げた物体がある。最初の状態における全エネルギーEはmgh。位置エネルギーがmgh、運動エネルギーは止まってるから０。和をとってmgh。
最後の状態、つまり地面に激突したときってのは、位置エネルギーが０、運動エネルギーが(mv^2)/2になる。そして全エネルギーEは変化しない。
じゃあ志津子さんに例題。
高さｈメートルのとこから物体を落下させました。地面にぶつかったときの速度は？

「え、私ですか」
不意を疲れた様子の志津子さん。
「えっと、今説明したのって、こうですよね」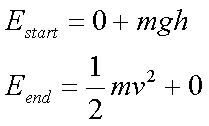

「そういうこと」
「えっと、変化しないんですよね。じゃあこれをつなげて……」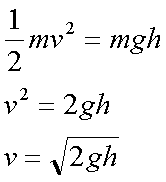

「こうですか？」
センターでもおなじみの解答だ。これはぱっと出せるようになってると便利だな。
「うん、正解」
「……あれ、落としたときの速さって重さによらないんだ」
と、稲穂。なかなかいいところに目をつけるな。
確かに重かろうが軽かろうが、地面についたときの速さは変わらない。
「だな。ガリレオの実験はこれを表してるってわけだ」
「へえ……」
志津子さんが感嘆する。
また一つ勉強になりました、と。

じゃ、まとめ。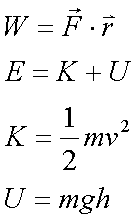

最後の位置エネルギーは地球上での重力による位置エネルギーな。
これについてはまた詳しくやろう。

「ねえ達哉」
稲穂が手を上げる。どうやら質問らしい。
「うん？」
「物体に力をかけると、加速度がつくよね」
運動方程式のことだな。
「ああ、そうだな」
「でも運動エネルギーもつくんだよね」
「そりゃそうだ」
今やったとおりだな。
「それでね、えっと……どうやって分けて使えばいいのかな？」
「分ける？」
何について分けるんだ？
「うん。えっと……上手く言えないんだけど、ぱこんってたたいても速さが上がって、ぐいぐい押しても速くなるってことだよね」
「あー、ああ。何となく分かってきた。じゃあ説明するか」

ま、答えから言ってしまうと、それぞれ積分してるものが違う。
まず、運動方程式から。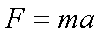

こうだよな。
で、速度の単位はこう。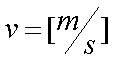

単位のｍと質量のｍを混同しないようにな。
でだ。運動方程式のほうの単位はと言うと、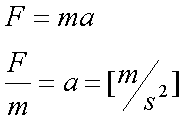

となっている。
ｓが－１乗多い……ってことはだ。
ｓの次数を上げてやれば、速度になるわけだ。
「時間で積分？」
「その通り」
そうすれば時間の次数が１つ上がって、速度の単位が出る。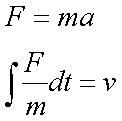

でまあ今更だがこれはこう。
力を時間積分すると、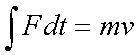

運動量だな。
一方、仕事の式は、
かけた力が全部運動エネルギーになるとすれば、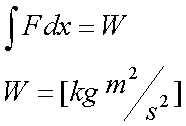

こうなるよな。
結局、力を距離で積分した場合は、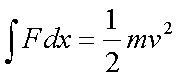

なんだし。
つまりは力があるとして、それを時間で積分すれば運動量変化。位置で積分すれば運動エネルギー変化ってわけだ。
とりあえずはそうやって覚えておけばいいんじゃないかな。
もちろん質量が分かっていれば、運動量から運動エネルギーを求めたり、逆も可能だけど。ま、定義から引っ張ってきた場合は上のようになるってことで。
あー、あんまり分かってないな。
まあこれはゆっくり考えてくれ。

「ただいまー」
ひと段落したところで、いつもの平和な声が聞こえてきた。
ひょいっと顔を出したのは、
「あ、佐倉さん」
「おかえり、お姉ちゃん」
「お邪魔してまーす、ゆかりちゃん」
佐倉ゆかりさん、２１歳。大学４年生。
「うん、いらっしゃい」
そう言ってにっこり笑うと、買い物してきた物を冷蔵庫に入れるため台所へ行ってしまった。
うーん、やっぱり佐倉さんはどこでも佐倉さんだなあ。
しばらくすると、とてとてと足音を響かせて、佐倉さんが戻ってきた。
「志津子、勉強の方は？」
「うん、なんとか。けっこう難しいね」
「そうか……」
よくついてきたとは思ったけど、やっぱり難しいか……
「あ、いえ、その新しい考え方というか」
そりゃそうだろう。高校でこんなに積分使って教えてたら笑うぞ。
あれ、でも万有引力のところは積分使わなかったっけか。
「志津子ちゃんは別のやり方で習ったの？」
「うん、全然。積分のせの字も出なかったもん」
「そうなんだ……」
まあ、それが普通だろうな。
稲穂に対してはスパルタだからな。スパルタ。
変な響きだな。スパルタ。

帰ろうとする俺を、佐倉さんが呼び止めた。
「あ、都君、お給料」
「え？」
すいっと差し出されたのは、茶色い封筒。
「家庭教師してもらったんだし」
「いや、そんな」
いくら入ってるか分からないけど、さすがにそれはまずいような気がする。
「ほら、交通費とかかかっちゃったでしょう？」
そりゃ、ちょっとかかったのはかかったけど……往復１０００円もかかってないし。
「うーん……じゃあ、交通費だけ。佐倉さんにはたまにご飯食べさせてもらってるし」
その食費だけで結構かかるような気がする。
「そうだけど……」
「今日はそのお礼ですよ」
しばし考えたあと、佐倉さんはにっこり笑って、
「うん、わかった。じゃあ、またお願いね」
と言ってくれた。
「はい」
というわけで、今日のお給料は１０００円。そしてまた家庭教師をする約束をして、その日は別れた。

戻る