|
Fox & Mathematics 〜べんきょう、しよう〜 力学初歩のお話2 パンパン! 静かな神社に柏手が響く。 「あ、達哉、おはよう」 お社の中から出てきたのは、いつもの稲穂。 「どこに入ってるんだ、お前は」 「ここしか寝るとこないんだもん」 お賽銭箱の横を抜けて降りてきた。 「はあ、さいですか……」 よく分からん奴だ。今に始まったことじゃないが。 「静かだしね。柏手以外は聞こえないんだ」 「なんだそりゃ」 「ん、まあよくわかんないけど、そういうところ」 まあ、科学では説明できんことは山ほどあるわな。 「…………」 その権化が目の前にいるわけだが。 「どうかした?」 視線に気付いて首をかしげる稲穂。 「いや」 事実はちゃんと受け止めないとな。うん。 駅への商店街を歩く俺と稲穂。 「今日はどこで勉強するの?」 夏休みの商店街。高校時代は見たこともなかった。だから高校生の姿がない商店街は、なんだか不思議な感じだ。 「我が母校」 「え?」 「志乃上高校」 「あ、そうなんだ」 交通費がかかるからと佐倉さんが悩んでいたらしい。そのくらい気にしなくてもいいのに…… まあ、稲穂の分の電車とバスを合わせると、やや重たい額になるが。 「あ、こんにちは」 「こんにちは」 と、駅で待ち合わせていたのは志津子ちゃん。 『さん』は他人行儀だ。と本人から言われたので、ちゃん付けで呼ぶことになった。 しかも、 「後輩だったとは」 そう。 志津子ちゃんはなんと、現役志乃上高生。正真正銘の後輩。 今2年らしいから、同じ時期に通っていたわけじゃないけど。それにしたって驚きだ。 「てっきりお姉ちゃんから聞いてるもんだと思ってました」 「いや全然」 「そうなんですかー」 というか、妹がいるってことも、夏休み入ってから知ったしな。 卒業以来の母校。 女の子二人にはさまれながらなんて、もちろん初めてだ。 「私服で良かったですよね。うちの学校」 「だね。制服だとばれる」 結局俺が制服を着たのは中学校のときだけってことになるな…… 普通の奴より半分ってわけだ。多分。 「でも先輩、知り合いの先生とかいるんじゃ」 先輩だって。 いや、当たり前なんだけどなんだか新鮮だなあ。 「うん、いるね」 「見つかったら」 「ま、なんとかなるでしょ」 笑って済ます。 そんな先生が多かったような気がする。 というか、卒業生は入っちゃだめ……なんて聞いたこともないし。全く部外者ってわけじゃないからな。むしろ、 「なんとかならないのは」 「私だけ?」 二人の視線を集め、首をかしげる稲穂。 ま、なんとかなるでしょ。 「はー、この坂、久しぶりだと疲れるな」 母校志乃上高校と、駅を結ぶ道。 長い坂があるのだが…… 「毎日だと慣れますよ」 そりゃそうだろう。 俺だって慣れた。いや、慣れていた。 「でも3年離れるとすっかり」 「運動不足ですか?」 「大いに」 言うとおり……だな。体育の授業なんて、1年の前期に取ってそれっきりだし。思えば高校時代はよく体育やってたよなあ。週2だか週3だか。 「あ、見えてきた。あれ?」 遠くに見える、見慣れた学校。 「だな」 それは懐かしさ漂う志乃上高校だった。 さて、無事校舎内に進入できた。 なんだか拍子抜けだ。まあ、夏休みにうじゃうじゃ先生がいるとも思えないが。 「図書室でしょうか」 と、志津子ちゃん。まあ無難なとこだな。 勉強してても怪しまれないし。 「かな。今日は開いてる日?」 「はい。そのはず」 夏休みも開いていたような覚えがちょっとある。 もっとも、現役時代夏休みに図書室を利用したかと言えば……ないんだが。 ちなみに大学に入ってからは、空調が効いているという理由から、長期休みはお世話になることが多い。 階段を上って、ちょっと歩けばすぐ図書室。 いや、懐かしい。 「誰もいないよ」 何の躊躇もなく、扉を開く稲穂。 怖い奴だ。 「ま、好都合」 俺たち三人は図書室に入ると、手近な机にノートを広げた。 さて、始めようか。 この前の続き……でもないけど、関連して力学的エネルギーの話の補足。 というかだ。先にばねの話をしようかと思う。 これがなんと言うか、基本の図。 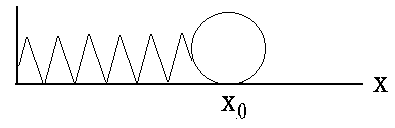 x0ってのは、つりあいの位置のことな。自然長とか呼ぶ。 で、とりあえずここを原点に取る。x=0ってことな。右がプラスで左がマイナス。ここからのずれをxとすると、物体にかかる力は、  こんな式で表される。 kってのはばねの強さによって変わる定数な。きついばねはkが大きくて、ゆるゆるのばねはkが小さい。 「一次関数?」 「だな」 すぐ数学に結び付けられるようになってきた。 なかなかいいことだ。 「見ての通り。力は場所の関数ってわけだ」 「うん。そうだね」 「じゃあ稲穂。ばねが伸びたとき」 ばねが少し伸びた図を書く。 「どういう力が働く?」 図とにらめっこする稲穂。やがて、 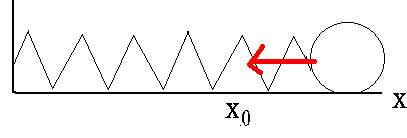 「……こうだよね」 矢印を書き込んだ絵を見せてきた。 「ま、そうだな。元の位置に戻ろうとする力。復元力が働く」 もちろん、ばねが縮んでいるときは反対方向に力が働く。なんというか、原点に向かって力がかかるわけだ。 kの前のマイナスはそのためな。 「じゃあ志津子ちゃん、この位置……x'とでもしようか。ここでの位置エネルギーは?」 「え、っと……この高さはいくつですか」 いきなり大ボケかまされた。 「いや、重力の位置エネルギーじゃなくて、ばねによる位置エネルギー。弾性エネルギーとか呼ぶけどね」 「ばね……」 あまりよくわかってない様子。どうしたもんか。 「んー、じゃあ、ばねから力はこうかかってゆくわけ」  ということはだ。 x'まで持っていくときには、こう力をかけなきゃならない。  赤いのがかけなきゃいけない力。式にすると、  と、いうことは? 「あ、えっと、積分でしたっけ」 「うん。やってみて」 力の関数は上の通り。 ま、積分は簡単だな。 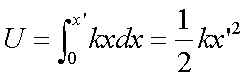 「……こうですか?」 予想通り、簡単に解けた。 まあ、一次関数の積分だもんなあ。 「OK。その通り。ばねによる位置エネルギーは、こうなる」 志津子ちゃんは何とか飲み込めた様子。 良かった良かった。 まあ見ての通り、エネルギーは二次関数。 グラフは適当に書くけどこんな感じな。  「じゃあ稲穂に問題。x'の位置まで引っ張りました。手を放すと元に戻ろうとする力が働きます」 「うん」 「原点での速さは?」 エネルギー保存だな。 前に教えたとき、志津子ちゃんがやったのと同じ。 「え、えっと……」 戸惑いながらも式を書き出す稲穂。 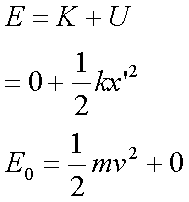 「こう、だよね」 一番上は全エネルギー。二段目はばねを伸ばしきった状態だな。 で、最後が原点での運動エネルギー。位置エネルギーはもちろんゼロ。 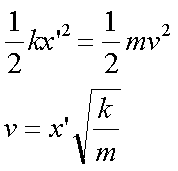 「えっと、向きは……ばねが縮む方」 「ん、まあいいだろう。よく出来たな」 「うん」 ほっと胸をなでおろす稲穂。 「でまあ、原点でスピードがあるってことはだ」 運動エネルギーが有り余ってる。 「縮みますよね……ばね」 と志津子ちゃん。 「うん。そういうこと」 運動としては、ずっとびよんびよんして止まらないわけだ。摩擦とか考えないから。さっきのグラフを持ってくると、ポテンシャルがこうなってるわけだ。  ポテンシャルってのはまあ、こういう坂があるイメージをしてみるといい。それにボールでも置くイメージをしてみると、右と左を行ったりきたりするよね。 結局は同じなんだよ。ばねの弾性エネルギーも重力の位置エネルギーもポテンシャルエネルギーだから、運動エネルギーに変わったり、運動エネルギーから変わったりしていくんだ。 で、これをばね振り子だとか、調和振動子だとか呼ぶ。格好いいから調和振動子って呼ぶことにする。 でまあ、この調和振動子。運動方程式はこうなる。 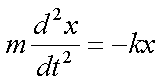 さて、これを解いてみようか。 解くってのは、xを求めることに他ならない。 あ、志津子ちゃんはこの式大丈夫? ……そう。加速度は位置の時間微分2階ね。右辺は力そのまんま。 でまあ、解くには見たまんま微分方程式を使わなきゃならんのだが……ま、このレベルなら大丈夫だろう。 まず、さっきの式を変形する。 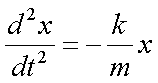 「さて、こう考えられる。係数はとりあえず置いておくとして、xってのは、tで2回微分すると、元の関数のマイナスと同じになる……こんな関数、あったよな」 シーンと静まり返る。 もしかして志津子ちゃん、2年だから三角の微分習ってなかったりするかも…… 「三角?」 「そうだ」 とりあえず、稲穂から答えが出た。 「2回微分すると……あ、そうか。そうですよね」 なんだか納得している様子の志津子ちゃん。ということは、大丈夫なのかな。 サインでもコサインでもいいんだが、とりあえずコサインを使おうか。 で、係数をこう置く。 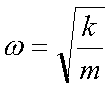 ωは普通『振動数』とか呼ばれるな。さて、代入するとこうなる。 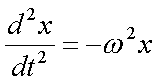 だから…… 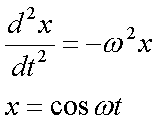 確認してみる。 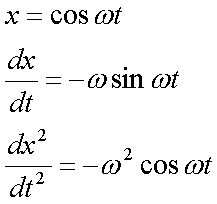 ん、OK。 分かると思うが、サインでもOKな。 つまりは、周期的な運動をすることになる。 「これでまあ、ばねにつながれた物体の挙動がわかったってわけだ」 「へぇ……」 「なるほど……」 必死にノートを取る二人。 うん、感心感心。 ちなみにこの調和振動子、いろんなとこで出てくるから。 さて、話はがらっと変わって、摩擦の話。 摩擦。まあ、俺たちが立っていられるのも摩擦のおかげ。 摩擦がなかったら恐ろしい世界になるな。 置いといて。 まあ、この力の正体ってのは分子間力。ファンデルワールス力とか呼ばれてるが、それはこの際どうでもいい。電磁気的な力だが、とりあえず置いておく。 でだ。摩擦は、物体の底面と床の間に働く。 図にするとこう。  赤いのが摩擦力な。大きさは、こうなってる。 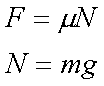 まんまだが質量mに比例な。 Nってのは床からの垂直抗力。まあなんというか、物体には重力がかかってるわけだが、上下には動いてないよな。つまりは床から同じだけの力で押されてるってこと。 で、摩擦はその力に比例する。 ちなみに、常に動いているほう(動かそうとするほう)と逆にかかる。 この辺はイメージしやすいと思う。 でだ。このμは摩擦係数と呼んでるわけだが、どういうわけか困ったことがあるんだ。 それは、止まってるときと動いてるときで、摩擦係数が違う。 動摩擦係数(μ)と静止摩擦係数(μ0)と言うんだが。 一般的には静止摩擦係数の方が大きい。 止まってるものの方が、動かすのが大変ってわけだ。 グラフにしてみるか。こんな感じな。 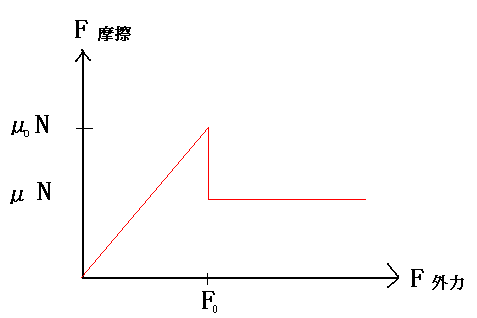 F0(=μ0・Nね)まで静止摩擦力が頑張ってる。で、限界に達して動き出すと、あとは動摩擦力が一定の大きさで働く。と。 じゃあ、この摩擦力とエネルギー。 上の図で、x動かしたときの摩擦のした仕事は? 「え? 仕事?」 「ああ、仕事」 「定義から行くと……」 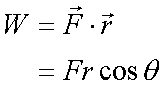 「ですよね」 志津子ノートに書き示される定義式。 「でも動いてる方向真逆だよ」 「ってことは?」 力のかかる向きと、動く向きの成す角は…… 「シータは……」 考え込む志津子ちゃん。 「360°?」 「1回転してどうする」 大ボケの稲穂。 「180°ですか」 「だね」 「ん? ってことは……」 稲穂ノートにぐりぐり計算。 大丈夫かな、こいつ…… 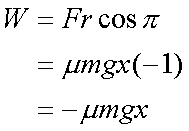 「仕事マイナスって……ありなの?」 「ありなの」 健闘空しく力がかかってるほうと逆に動いて行った場合、その力のした仕事はマイナスになる。 「うーん……」 「ま、分かりやすく言うと……ずりずり押してるわけだが、摩擦があるせいであんまり動かないよな」 「うん」 うなずく二人。 摩擦がある運動は実際に見れるから、イメージしやすいだろう。 「本来ならもっと速く動けていたわけだ。ところがどっこい摩擦のせいで速く進まない」 「あ、じゃあその差? ……あー、そっか。本当の運動エネルギーから引くんだ」 なんとなくわかった様子。よかったよかった。 「ま、そういうことだな。ちなみに摩擦で使われたエネルギーは、熱やらなんやらになってどっかいってしまう。保存力じゃないってわけだな」 んー、じゃあ最後に、慣性力の話をして終わろうか こりゃまた説明のしづらい面倒な力なんだけど…… 志津子ちゃん。バスに乗ってて、急ブレーキがかかったら、どうなる? うん。前につんのめるよね。 加速度の働いている系を加速度系と呼ぶんだけど、あ、つまり加速中の電車やらバスを想像してみればいい。 急ブレーキってことは、後ろに加速度ね。前の速度が減ってるんだから。 で、加速度系でaという加速度がかかったとき、系の物体には、 こんな力がかかる。  系の加速度と反対方向な。 図示すると、こう。 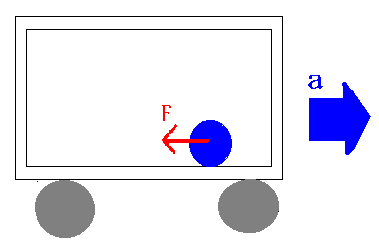 でまあ、これはいろいろ扱いが難しいんだよね。 何によっての力なのかわかんないでしょ? 見かけ上の力だとか、ややこしい議論があるけど、まああるものと思ってくれ。 でまあ、加速度系の反対の言葉は、慣性系。 等速運動している系と、静止してる系は運動的に区別できないから。 まあ、こういう力が働くということで。 まあ、この辺まで。 今回のまとめ。 ばねの弾性エネルギー。  摩擦力。 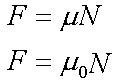 で、慣性力。 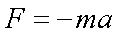 次はどうしようか。 みっちり力学やってもいいけど、他のもやっといたほうがいいだろうしなあ。 はあーっと二人が息をついた。 ちょっと急いだ感はあるな……教えるのも少し疲れる。 改めて回りを見回す。 誰もいない図書室。懐かしい空気。聞こえてくるのは時々通る車の音だけ。今日は部活もないらしい。 そんな静かな空気が破ったのは、ドアが開く音。 誰が入ってきたんだと顔を向ける前に、声が飛んできた。 「こら部外者」 「えっ!?」 バレた!? 俺か? 稲穂か!? つかつか歩み寄ってくる声の主に、俺は見覚えがあった。 というか、 「なんだ、よりりんか」 担任だった。 「そうさ、よりりんさ。みゃーこ」 不敵な笑みを浮かべて、恥ずかしいニックネームを呼んできた。 声の主は雲浦依子先生。通称よりりん。 1年と3年のとき担任だった。担当教科は数学で、授業では3年間通じて数学のお世話になった……時々稲穂への説明に出てくる『神経質な数学屋』とは、何を隠そうこの人のことだ。 「みゃーこはやめてくださいよ……」 丸いめがねをくいっと上げると、楽しそうに笑う。 「先にニックネームで呼んだのはどっちかな」 無造作に束ねられた髪、化粧っけのない顔。おおよそ色気というものが感じられない。でも、だからだろうか。俺たち生徒との距離はほんと短く感じたんだよなあ。ニックネームで呼び合うことにも違和感はないし。 「みゃーこ?」 首をかしげる稲穂。 しまった。懐かしさに浸っている場合じゃなかった…… 「都がなまってみゃーこ。で、なにやってんの、みゃーこ?」 物珍しそうに机の上を覗いてくる。 そこには広げられた稲穂ノートと志津子ノート(仮)。 「だからみゃーこは」 「かわいい」 「うるさい」 口を挟む稲穂。 さて、どう説明したものか…… 「えっとまあ、家庭教師の家庭じゃない版ですよ」 なんだそりゃ。心の中でセルフ突っ込みを入れる。 「そりゃ教師じゃないか」 ……ごもっとも。 「まあいいや。でまあ、この現役お二人さんに勉強を教えていたと。両手に花だね」 どうやら稲穂のこともここの生徒だと思っている様子。助かった…… さて、その現役お二人さんはというと、 「花だって、志津子ちゃん」 「ですって、稲穂さん」 手を取り合って仲良くしていた。 ああ、幸せそうで何よりだ…… 「で、よりりんはこの夏休みの学校へ何しに?」 しかも図書室。 「あたしは毎年恒例のアレをね」 「ああ、アレか……」 文化祭のアレですか…… 「でまあ、細かいところをちょっと忘れたから、図鑑でもないかと探しに来たわけさ」 「はあ、なるほど」 「ちなみにみゃーこの年よりも大きいわよ」 まあ、細かいところってんだからそうだよなあ。 ちなみに俺の代では手のひらサイズだった。 「毎年巨大化?」 「はは、そろそろ極大値だねえ」 ちなみに普通の人は極大値なんて言葉は使わない。 「小さくなっていくのか。で、5年後ぐらいは小指の爪に乗ったり?」 「その前に極小値があるでしょ」 よりりんならやりかねんが…… 「何次関数ですか」 「発散させる気? 三角よ。きっと」 あー、それもそうか。発散したらえらいことになるな。 「えらく長波長……ってか、重ね合わせてるだけかもしれませんね」 「あはは、みゃーこも上手いこと言うようになったねえ」 けらけら笑うよりりん。 卒業してから3年経ったってのに、相変わらずだなあ。 「……どうしよう、凄い変な会話してる」 「でも意味はわかるよ」 「そりゃ、分からなくもないけど……」 ついてこれてるのか分からない二人。 その二人のノートを覗き込むよりりん。 なぜだか俺が恥ずかしい。 「ふうん、物理ねえ……次は何するのさ」 「そうだなあ……」 考えてなかった。 何がいいかなあ。 そうだな。 「円運動やってから、重力の話ですかね」 「ほうほう。そりゃ興味深い。ってか、受験に使うのかね」 「さあ、出ないような気もする」 というか、量子までの道のりで必要なのかも分からない。 「ま、いいけどね……と、図鑑探してくるわ。気が向いたら文化祭に来なよ」 そう言うとよりりんは俺たちの机から離れて行った。 「……じゃあ、そろそろ帰るか」 「あ、うん」 「そうですね」 クーラーの軽く効いた図書室。 離れるのは名残惜しかったが、いつまでもいるわけにはいかない。 割と居心地も良かったし、また使わせてもらおう。 そんなことを思いながら、我が母校、志乃上高校を後にした。 戻る |