Fox ＆ Mathematics 　　　　　〜べんきょう、しよう〜 　　極座標と円運動のお話 久しぶりに稲穂と二人きりだ。 「志津子ちゃんは？」 「今日は来ないって」 なんでも物理はそこまでやらなくてもいいらしい。生物系だか薬学系だか志望なんだそうだ。 「ふーん……」 ……前回やりすぎたかも。 ここは志乃上高校正門。 都合よく図書館の開放日だったので、ありがたく使わせてもらうことにする。 多分人はいないと思うんだが…… 「あ、ちなみに」 稲穂が振り向いた。 「出来るだけさっさと終わらせるからな」 すると稲穂は、 「わかってる」 とにっこり笑った。 たどり着きましたるは図書室前。 「誰もいないといいね」 「ああ」 言いながら扉を開くと、 「…………」 人がいた。 ガラガラ……ピシャ 無言で扉を閉める稲穂。 「ひ、人がいたよ！」 「そらいるだろうよ……開放してるんだから」 ま、あんまりやかましくはできないか…… 少し気を使いながら勉強するか。 再び扉を開く。 中にいるのは……一人。髪の長い女の子だ。床に座り込んでなにかしている。 「…………」 めちゃくちゃ緊張している稲穂。 こういうものは、逆に堂々としている方がバレないもんなのにな。 「行くぞ、稲穂」 「た、達哉……」 腕にがっしり掴まる稲穂。 ……歩けないじゃないか。 入り口でもたもたしていると、女の子が振り向いた。 「……？」 俺たちを見て不思議そうな顔をする。 「ほれ、歩け」 「う、うん……」 ずりずりと稲穂を引きずるように机に歩いてゆく。 その途中、稲穂と女の子の目が合った。 「あ、こ、こんにちは……」 不器用な笑顔で稲穂が挨拶した。 まんま不審者だ。 「あ、はい。こんにちは」 律儀に返事が返ってきた。 「……」 「……」 会話終了。 一体何がやりたかったんだ、稲穂…… 「ああ、俺たちのことは気にしなくていいから」 「あ、は、はい……」 そううなずくと、女の子は再び作業に戻った。 この角度からはよく見えないが……絵を描いているんだろうか。 ま、いいか。 「ほら、稲穂、さっさと用意しろ」 「う、うん……」 こいつ、意外とビビリ屋だな。 稲穂ノートが開かれる。 さて、今日の授業開始だ。 今日は……円運動の話。 というか、便利だから極座標の話から入ろうか。 例えば稲穂。 グラフ上に原点とある点の位置を考える。 普通どう表す？ 「え、ｘｙｚじゃないの？」 「そうだよな。それがまあ楽だ」 だが場合によっちゃ、こんな表し方の方が便利だったりする。 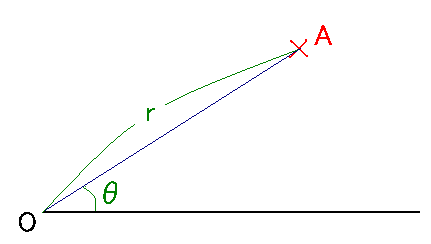ここで決まってるのは、原点からの距離と角度。 ｘｙの代わりにｒθを使うわけだな。 「へえ、なるほどね。確かにこれでも位置はわかるね」 ふむふむとうなずく稲穂。 これで図形なんか表す場合は、例えば、 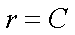なんてのがある。 これは原点からの距離がCである点って意味だな。どんな図形かと言うと、 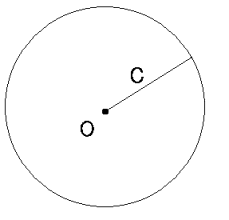こんな奴。まあつまり円だ。 あるいは、 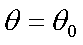こんなの。 まあ分かると思うが、 こんな感じ。 左下に伸びてないのに注目な。左下に伸びるのは角度がπ違うから。 じゃあ、ちょっと問題。 こんなので表された図形はどんなのか描いてみろ。 「え……うん」 じっと式を見つめる稲穂。 「rが増えると……角度も増えるんだよね」 「最初の点は、どうなってる？　０のところ」 「えっ、そりゃあ、原点よね」 「じゃあ、そこから長さの絶対値を増やして、角度も増えた点を取ってみろ」 「……うん。えっと」 「反時計回りになるほど、原点から離れていく……」 稲穂って図を描くときぶつぶつ言う癖があるんだよな…… 「ああ、その調子」 「あ、なんか分かってきた」 こいつ物分りいいよな…… 「ん、じゃあそれをつないでみろ」 「うん」 「なんかへたくそになっちゃった」 「気にするな。流れが分かればそれでいい。図形としては、」 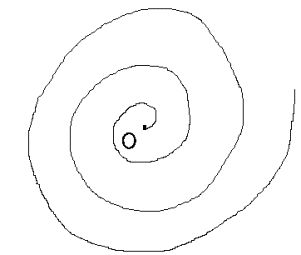「こんな感じになる」 「あはは、達哉もへたくそだ」 げらげら笑う稲穂。くそう…… 「ほっとけ」 手書きなんていびつで当たり前だっての。 「ふーん、面白いね」 「だろ？　じゃあこのｒθとｘｙはどんな関係になってる？」 最初の定義を思い出したら分かるよな。 「え？　ど、どんなって……」 「サインコサインでやったじゃないか」 「あ……あー、そっか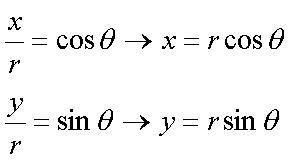！」 「おっけーだ。よく覚えてたな」 「えへへ……」 この変換さえあれば怖いものなしだ。 ……３次元は今日はやめておくか。 ま、これを基本としてだ。 原点から等距離で円運動する物体を考える。 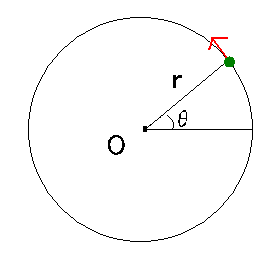ここでの物体の運動は、こう表される。 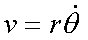「この点なに？」 稲穂がθの上のドットを指差した。 「あれ、説明してなかったっけか。時間微分のことだ」 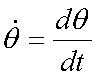ｄだのｄｔだの書くのが面倒だから、点で表すわけだ。結構使うから覚えとけよ。 「点って前も使わなかったっけ。微分で……ほら」 稲穂ノートをぱらぱらめくる稲穂。 点って…… 「え？　あー、ああ……」 ダッシュのことか。 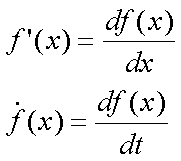「これな」 普通、上のドットは時間微分を表して、ダッシュは位置での微分を表す。 よく使うから覚えとけよ。 で、話を戻す。 速さｖは見てのとおり、ｒとθの時間微分の積になってる。 もちろん角度が増えていくのが大きいと速いし、同じ角度の増え方でも原点から遠いほど速い。 ま、その辺はイメージで分かるよな。 じゃあ、位置をｘｙとして、そこから速さを求めてみるか。 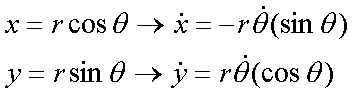今回ｒは一定だから、積の微分でｒを微分した項は０な。 一定のものを微分したら０。これは鉄則中の鉄則な。しっかり覚えとけ。 でだ、ベクトルの大きさってのは、いつだって求め方が決まってる。 つまり、各成分を二乗して足すわけだな。それがベクトルの大きさの二乗になってるから。 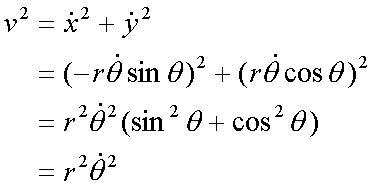ここから、 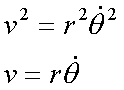ってなわけだ。 で、このθの時間微分を、特にωと置く。 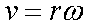こうすると、まあすっきりするんだ。このωを角速度と呼ぶ。 もうちょっと付き合え。 この角速度はこうなるよな。 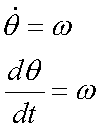「こうなるよなって、今言った通りじゃない」 不思議そうな顔をする稲穂。 「まあそうなんだが……でだ。微分のｄｔを取り除きたいんだが、どうすればいい？ 「どうすればって……どういうこと？」 ちょっと抽象的だったか…… 「ま、こういうことだ」 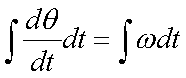「あ、なんだ。積分かあ」 計算するとどうなる？ 「そんなの簡単だよ」 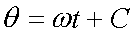ま、そんなとこだな。 で、これを踏まえたうえで、最初のｘｙを書き換える。 Cは初期の角度になるんだが、今回は０でいい。 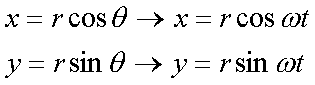「あれ、この形……」 気付いた稲穂。 覚えてたか。 「一緒だね。ばねのときと」 「ああ、そうだな」 つまりはこうなるわけだ。 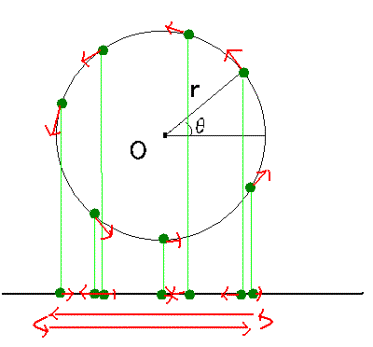……変な点の取り方で見づらくなったな…… 「あ、き、気持ちは分かるから大丈夫だよ！」 困った笑顔を向ける稲穂。 い、稲穂にフォローされるとは…… 「ま……まあ、ばねの振動は、円運動の射影ってわけだ」 とりあえずそう締めくくっておく。 そんでまあ、ωってのは、単位に直すと[rad/s]となる。まあ、１秒で何ラジアン進むかって奴だな。 で、これから１周するのにどれだけ時間がかかるかわかる。 さて、１週にかかる時間を求めるにはどうすればいい？ 「えっと、１周は……２πだったよね」 「だな」 「ωが……例えばπだったら、１周するのに２秒かかるよね……じゃあそのまま割ればいいのかな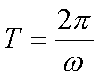？」 「ん。OKだ。このTを周期と呼ぶ」 「でだ。１周するのにかかる時間がTだとすれば、１秒間に何周できるかもこれで表すことができる」 「え？　１秒間に？」 「ああ。まあ、単位を見ればすぐわかるんだが」 Tはもちろん[ｓ]だよな。１周にかかる時間なんだから。 で、１秒あたり何周かってことはだ。[1/s]の単位になる。 だから、 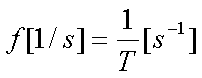このｆが１秒間に何周できるか……つまり振動数ってわけだ。 「うー、頭がこんがらがってきた」 じゃあ、整理するために例題でもやってみるか。 １秒で円を５周する物体がいる。 これの角速度ω、周期T、振動数ｆを出してみろ。 うっわ……なんか大変そう。 と、５周なんだよね。５周５周…… １周するのが２πだから、５周は１０π。 角速度……だっけ。ωは１秒間に何ラジアンだから…… 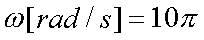かな。 えっと、それからTは…… 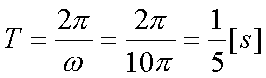えっと、これってつまり、１周するのに0.2秒かかるってことよね。 ふんふん。 で、最後はｆ…… 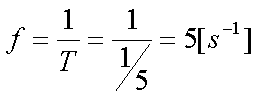だから、1秒間に5回転……って、初めに聞いた通りじゃない。 「ん、大丈夫だな」 よしよし、ちょっと簡単すぎる気もするがまあいいか。 さて、最後に運動方程式に当てはめようか。 「え、まだやるの？」 「最後だって」 さっきのｖがある。 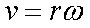まあ、このままじゃいじりにくいから、さっきのｘｙを引っ張ってこよう。 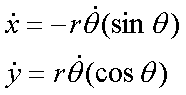もう１回微分できるよな。 やってみろ。 「あ、うん」 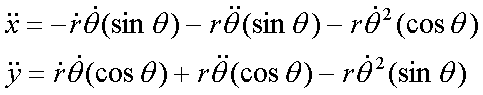えーっと、ｒを微分した項があって、θを微分した項があって、最後の三角を微分した項……か。よしよし。中身の微分を出すことも忘れてないな。 「おっけーだ」 割と計算力もついてきたかな…… 「さて、ベクトルの絶対値を出す」 「また二乗？」 「その通り。やってみろ」 ……とはいえ、ちょっと項が多いな。 「うん……ちょっときついね」 「まあな」 さて、どうしたもんか。 3^2項が２つで18項か……稲穂の奴、泣きそうになりながらがりがりやってんな。 開いてみると、 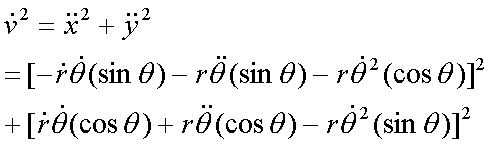この時点で消えるのは、ｒの時間微分。原点から等距離だからな。 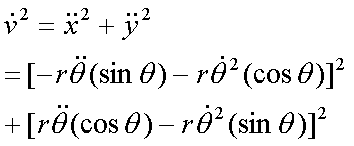でまあ、展開してもいいんだが、等速円運動って事を忘れちゃいけない。 等速って事は、ｖの大きさは変わらない。 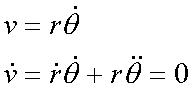１項目はｒの時間微分で０、で、２項目も０にならなきゃいけない。ｒは０じゃないから、θの２回時間微分も０。 よって、 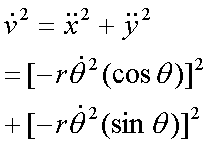この項だけが残ると。 もちろん答えは、 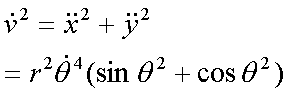だから加速度の大きさは、 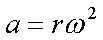とまあ、こうなるわけだ。 「ひっどーい、解説してよ！　全部足したり引いたりして計算しちゃったじゃない！」 ノート1ページにわたって計算した稲穂がぶーたれた。 「うるさいな……計算練習だと思え」 こういうのは、手を動かしてナンボだ。 図で表すと、こうなる。 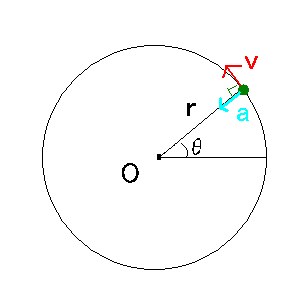で、加速度の大きさが求まったところで、改めて運動方程式に代入する。 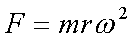方向はもちろん加速度と同じだから、常に中心に向かって力が働いていると、円運動になることが分かる。 「どうした？」 なんか腑に落ちていない様子。 「え、うん……なんていうのかな、ちょっとわかんないところが」 「どうした？」 俺のメモをじーっと見ている稲穂。さっきの加速度を求める過程だ。 「達哉の計算の途中で、ｖの時間微分は０って言ってたよね」 「ああ」 「じゃあ加速度は０じゃないの？」 なに？ ……ああ、そういうことか。 「いや、それはだな……ｖの大きさは時間に対して不変だって言ったんだ」 「うん」 「成分の大きさは変わってるだろ」 「あ……あ、そっか」 等速円運動ってのは、速度の絶対値が変わらないってことだ。速度の方向はそりゃあ時間によって変わってる。 まあ、分かったみたいだからいいか。 ん、じゃあまとめ。 極座標。 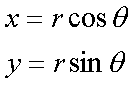等速円運動。 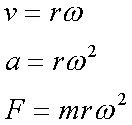これは大きさであってベクトルじゃないからな。 ちなみに向いてる方向は、ｖが接線方向、Fとaは位置ベクトルに逆向きな。 「終わり。結構時間かかったな」 「うん、急いでいかないとね」 勉強道具をしまいこみ、席を立つ。 入り口まで来ると、稲穂とさっきの女の子の目が合った。 「あ……」 何をやってたのか知らないけど、ぼそぼそしゃべってたのは迷惑だったかもしれない。 ごめんよ現役生。 「うあ……えっと、さよなら」 「あ、はい……」 ガチガチになる稲穂に、その子は小さく頭を下げた。 「ああ、怖かった」 ほっと胸をなでおろす稲穂。不審者め。 「お前は小動物か」 「近いものはあるかも……」 なんだそりゃ。 「やれやれ……」 というわけで、学校を出た俺たち。早歩きで駅へと向かう。約束の時間には……ちょっとシビア。 坂を下ると志乃上駅。志乃上駅から２駅で草神駅。到着した俺たちを待っていたのは、佐倉さん。 麦わら帽子に半そでＴシャツ。なかなか活動的な格好だ。 「ゆかりちゃん、帽子似合ってるよ」 「そう？　ありがと、稲穂ちゃん」 と、３人集まったのは他でもない。 夏休みスペシャル企画、みんなでハイキング！　というわけだ。 「それで……どのバスだっけ」 「えっと」 バスターミナルになっている草神駅。 いくつかバスの行き先がある。 「……山之口提延寺行きかな。だから、あっちの乗り場ですね」 本数があるのかどうか結構心配だったけど…… 「あれに乗るの？」 と稲穂が指差す先には、停車中のバス。 そうだ。それに乗るんだよ。 「ラッキーだったね」 と、ニコニコの佐倉さん。 「ええ、でも１５分に１本出てるから、そうでもなかったかも」 「でも１５分待つよりはいいよ」 「そうですね」 稲穂はというと、なにやら緊張している様子。 「……」 何でバスに乗るのに握りこぶしなんだか。 どうもこいつ、公共交通機関に弱いよな…… バスが走ること２０分少し。 「次は登山口です」 目的地は次だそうだ。 周りを見渡すと、もう一面畑。草神駅から少し離れるとこんな感じ。 草神の代表的な農産物はキャベツだ。 小学生のときに習った。なぜかそれだけははっきり覚えている。 「んー、着いた着いた」 バス停の目の前に山。 左右と後ろにはキャベツ畑。 これでこそ草神だよな…… 「わーい」 ふと見ると、全速力で山を駆け上がっている稲穂。 「子供か、あいつは……」 「ふふっ、稲穂ちゃん、そんなに急ぐとバテちゃうよ」 佐倉さんの声に振り向く稲穂。 「大丈夫大丈夫！」 手をぶんぶん振ると、また坂を駆け上がる。 「ったく……」 俺と佐倉さんは顔を見合わせた後、小さく笑って山を登り始めた。 「なんだか懐かしいね」 「そうですね」 のんびりと歩く俺と佐倉さん。 草神市の代表的なハイキングコースであるここは、市内の小学生の格好の遠足スポット。 草神市民のほとんどは小学校時代にここの山登りを体験するわけだが、俺も佐倉さんも例外ではなかった。 「暑……」 しっかり照り付けてくる８月の太陽。 何度も汗をぬぐう。 「はーやくー」 はるか先から聞こえてくるのは稲穂の声。 「稲穂ちゃん、もうあんなに遠くに……」 「張り切りすぎだ……バテるぞ……」 稲穂にせかされて、ペースを上げる。 思えばこれが失敗だった。 「ぜえ、ぜえ……」 ほら言わんこっちゃない。 しっかりバテていた…… 「大丈夫？　達哉」 俺が。 「はぁ、はー……はーぁ」 佐倉さんもだった。 「しっかりしてよ、二人とも」 「そんなこと、言っても……」 ゴールは見えているんだが、どうにも足が動かない。 「なんでお前は平気なんだよ……」 「え、このくらいへっちゃらだよ」 言ってぴょんぴょん跳ねる稲穂。 なんだこいつ…… 「ぜえ……運動不足のツケだ」 「ほんとにね……普段運動なんて、しないから……」 へろへろの大学生２人。 「ちょっと休む？」 「ああ、そうだな……」 ああ、疲れた。 ほんと、なまってるよなあ。 「小学生より弱いかも知れない……」 隣で佐倉さんが落ち込んでいた。 麦藁帽子を深くかぶっているのは演出だろうか。 「いや、それはさすがに……」 しかし、小さい頃はよく弱音も吐かずに登りきったな。 まあ、遠足自体が珍しくて、浮かれたままのテンションで登ってただけかもしれないが。 「あ、ゆかりちゃん私もお茶飲む」 それにしてもこいつ……丈夫すぎ。 「稲穂……お前、体力あるな」 「え、まあね。でもお母さんや姉ちゃんの方がもっとすごいよ」 興味あるが……まあ、人間離れしてるもんなあ。 「そんなにすごいんだ」 「うん。山の４つや５つは軽く超えちゃうもん。本気出したら一日中走っても平気」 どんなだ…… その割に自転車使うんだな。 と聞いてみたところ、 「そりゃ、自転車の方が速いし疲れないから」 だそうで。なるほど。 とまあ、紆余曲折を経て、頂上までやって来た俺たち。 「ひゃあー、いい眺め！」 相変わらずはしゃぐ稲穂と、 「ほんと。気持ちいいねー」 復活した佐倉さんと、 「ああ……」 疲れたままの俺。 「ねえねえ達哉！」 稲穂の奴、はしゃぎまくりだな…… 「うん？」 「今すっごいポテンシャルエネルギー高いよね！」 「……ああ」 稲穂の頭の中もずいぶんと励起されてるようだな…… とはいえ、頂上からの眺めはかなり良い。 学校のある丘やら、草神駅を中心としたビル街。 周りを取り囲む田畑。 正しく草神市を一望といったところだ。 小さい頃に見たはずの景色だが、その時のことはよく覚えていない。 もう１０年ぐらい経ってるからな……そりゃ変わってもいるだろう。 「お腹すいた。お弁当お弁当」 ……人が感傷に浸っているときに、こいつは。 佐倉さんと顔を見合わせて、ふっと苦笑い。 確かに昼ご飯食べてなかったから、腹は減っているが。 「やったー、いなりずしー！」 ま、それも俺たちらしくて良いか。 自分の育った街を見ながらのお弁当ってのも、なかなか良いもんだし。 ちょっとした屋根付きのベンチで３人で食べるお弁当。楽しそうな稲穂と佐倉さんを見て、やっぱり来て良かったなと思った俺だった。 まあ、翌日しっかりと筋肉痛が待っていたわけだが。 なまってるよな、ほんとにもう…… 戻る