|
Fox & Mathematics 〜べんきょう、しよう〜 万有引力と角運動量のお話 本屋から家に帰る直前だった。 我が家の玄関の前に、なにやら人影が見えた。 「お留守かしら。困ったわ……」 女の人の声……母さんではない。でも、どっかで聞き覚えある声だ……うーん。 恐る恐る覗いてみると、 「あっ」 「あら」 その人と目が合った。 「お久しぶりです」 にこっと笑うその人。 「あ、は、はい……どうも」 どうしてこんなところにいるんだろう。 ってか、なんで俺の実家に? 実家は教えてないはずだけど、でも俺を訪ねてきてるっぽいし……? 「どうかしましたか?」 混乱する俺に、余裕の笑みを浮かべる稲穂の母、穂香さんであった。 「……どうやってここが分かったんですか?」 とりあえず穂香さんを居間に通すと、麦茶を出しながらそう聞いてみた。 「あら、携帯電話の番号を教えてくださったでしょう? それさえわかればちょちょいのちょいですわ」 「そ、そうすか……」 あえて追求しない。 深く関わらない方がいいような気がしてきた。 「それでまた、今日はどうされたんです?」 「ええ、稲穂の様子を聞きに」 稲穂の様子……か。 まあ、相変わらずなんだけど。 「特に変わりないですよ」 「そうですか。あと、都さんからの客観的な評価がお聞きしたくて」 「評価……ですか」 勉強の方だよな。 「前にも言いましたが、それなりによくやっていますよ。あいつは。勉強も好きになってきているみたいですし」 「そうですか……」 それを聞いて、どういうわけか複雑な表情の穂香さん。 「どうかされましたか?」 なんとなく聞いてみる。 「ええ……」 何かを言おうかどうか、迷っているようにも見えるけど…… そのとき、玄関でばたばたと音がした。誰かが帰ってきたようだ。 「ただいまー」 聞こえてきたのは母さんの声。 「げ……」 その足音は一直線にこっちに向かってくる。 そして入り口から、見慣れた顔がひょっこり顔を出した。母上だ。 「あら、たっちゃん……と、そちらは?」 当然のごとく穂香さんを見て首をかしげる。 「はじめまして。音羽穂香でございます。都さんには常々お世話になっております」 ま、紛らわしい挨拶を…… 「あ……あらあら、これはご丁寧に。達哉が? えーと……」 なにやら考えている様子。 そして、勘違いな結論に至ったようだ。 「はあ、たっちゃんもそういう年頃だもんねえ」 聞こえてるっての。 「穂香さん……でしたか。社会人でいらっしゃいますか?」 「社会人……ええ、まあ、そうですわね。沼崎の方で働いております」 そうだけど……そうだけど! 「そうですか。変な子ですけども、達哉の事、よろしくお願いします……」 「いえ、こちらこそ……」 なんだかよく分からないままに、ご挨拶が済んでしまった。 そりゃあまあ、どっからどう見ても二女(もっといるのかもしれないけど)の母とは思えないぐらいの若さだけどさ…… つーか、穂香さん作為的すぎ! 「では、私はそろそろ」 穂香さんが音もなく腰を上げた。 「あら、もう行かれるんですか? もっとゆっくりしていっても」 「いえ……もともと仕事の途中で寄ったものですから」 嘘だよなあ…… 「そうですか」 「はい、ではまた……」 わけのわからないまま、電撃訪問は終わった。 立ち尽くす俺と勘違いの母上を残して…… とまあ、こんなことがあったわけなんだが。 「お母さんが……」 じっと考える稲穂。 ここは志乃上高校図書室。クーラー付き。 「ああ、どういうわけか」 「何か言ってたの?」 「んー……」 何か言いたそうだった穂香さんの表情を思い出す。 「いや、特に何も」 とりあえず、そう言っておくのがいいような気がした。 ノートを広げる。 「さて、今日は万有引力の話だ」 「りんごがどうとかいう話?」 「……それは別にどうでもいい」 地球上での物体の運動ってのは、重力を受けているわけだよな。 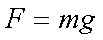 この式だ。 実はこれは、近似式であって、万有引力による力ってのは、こう表される。 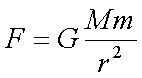 Gは万有引力定数。重力定数とも言うな。Mが物質Aの質量でこの場合地球の質量、rが重心からの距離。 この式が表すところは、つまりだな……2つの物体の間に働く力は、質量が大きいもの同士の方が大きい力になる。で、距離が近いとまた大きな力になる。 rが2乗になっているが、これはつまり…… 「距離が離れると、ものすごい勢いで弱くなっていくってこと?」 「あたり」 で、今『地球上』って言ったが、これがミソなんだ。 地球の半径は6378km。つまり俺たちのいるこの場所は、地球の中心(つまり地球の重心だな)から6378km離れてるってことになる。 地球の質量は5.97×10^21トンだそうだ。 さて、代入してみるか。 万有引力定数は……理科年表によると、6.67×10^(−11)単位はm^3/kg・s^2らしい。 でだ、よく気をつけなきゃいけないことは、単位を合わせること。 トンだのキロだのが入り乱れてるから、MKS……つまり、メートル、キログラム、秒に直さなきゃいけない。 改めて、 M:5.97×10^24[kg] r:6.378×10^6[m] 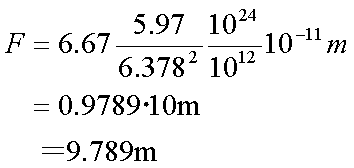 な、だいたい9.8になっただろ? 「うん。大体そうだね」 まあ、本当は自転の遠心力がかかってもう少し違う値になるんだけど……それはおいおい稲穂が気付けばいいか。 「さて、力がかかってるんだから、調べることは分かるよな」 「え?」 「早速重力によるポテンシャルエネルギーを求めろ」 「あ、うん……えっと、力を位置の関数として……位置で積分するだけだよね」 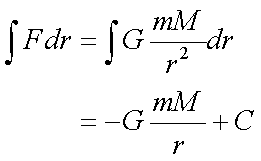 「おっけーだ」 さて、このCをどうするか 中心力ってのは、大体無限遠で0になるようポテンシャルの基準を決めるんだ。C=0ってことな。 で、イメージできると思うが、2つの物体が近ければ近いほど、かかる力が大きくなって、どんどん真ん中へと引っ張られてゆく。 物体が引っ張られるってことはだ。そっちの方がエネルギーが低くて安定だからそっちに行く……つまり、中心でポテンシャルはマイナスの無限に落ちてる。 ……グラフにすれば分かりやすいかな。 こんな感じ。一次元だが。 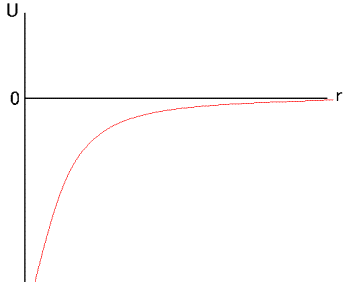 な、無限遠で変にプラスになっても計算しづらいだろ。 重力によって物体が引っ張られていくってことは、この赤い曲線を、物体が滑り落ちていくのを想像すればいい。中心付近でものすごい勢いで落下するよな。 「うん。なんとなくわかる。これだったら確かに、無限で0になった方がいいよね」 「よしよし」 で、力学とくればエネルギー保存。 運動エネルギーとポテンシャルエネルギーの和が一定だっていう話だよな。 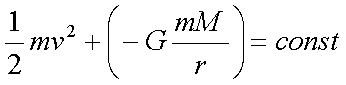 別にこれはどうでもいいな。ただのエネルギー保存則。 遠くにいたら遅くて、近くに来たら速くなるってだけだ。さっきの曲線グラフ見れば分かるよな。 さて、実際重力で運動しているものと言えば、代表格として惑星がある。地球が太陽の周りを回ってるのは、重力のおかげだって言う話だな。 これについて、ケプラーって人が3つの法則を見出した。 惑星は太陽を焦点とする楕円軌道を回る 惑星と太陽を結ぶ線が一定時間に通過する面積は一定 惑星の公転周期の2乗は、軌道の3乗に比例。 この3つは、ケプラーの3法則と呼ばれたりする。 まず最後の法則を証明しようか。 さて、前回の復習。円運動で中心に向かう力はどうなってた? 「えっと……」 稲穂ノートをぱらぱらめくる。 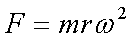 「これ?」 「そうそれ。で、さっきの重力の計算式を当てはめてみるとどうなる?」 「えっと……」 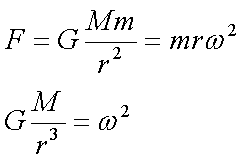 mを消して、rを移項……と。 「そう。それが出るよな。周期と角速度の関係は?」 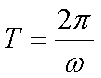 「これ?」 大活躍の稲穂ノート。 「そうだな。そっからどうなる?」 「えっと……」 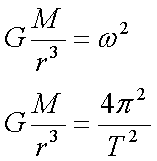 「つまりこれは」 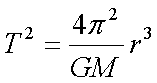 「な、周期の2乗は半径の3乗に比例してるだろ?」 「ほんとだ」 いや、いつ見てもきれいだ。 「実際グラフにすると、こんな感じになる」 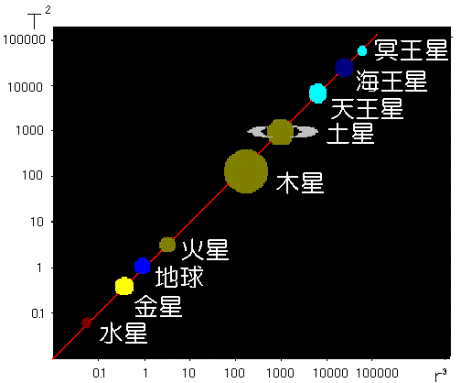 宇宙だから背景黒にしてみた。 だからどうというわけじゃないけど、赤い線の上に載ってるよな ほんとは楕円運動だからrじゃなくて長半径を使うんだけど、ま、あまり深く気にしない。 さて、2番目の法則を証明したいところだが、まずは角運動量の話から入ろうか。 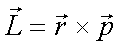 こんな量がある。Lを角運動量と呼ぶんだが、外力が働いてない系の場合は、これもまたエネルギーやら運動量やらと同じく保存する量なんだ。 それも、かなり強力な保存の仕方だ。 ま、具体的な話に行こうか。 図にすると分かるが、角運動量はこんな感じ。 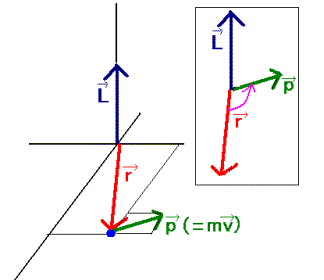 式見て分かるだろうけど、外積だから運動量ベクトルと位置ベクトル両方に直交な。rからpは基本の回り方。だからLは上向き。 xy平面として考えると、Lはz成分だけになって、こんな式で表される。 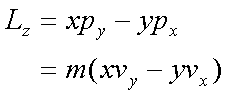 さて、式を極座標に変形すると、 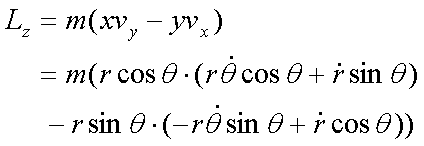 長い式だけどこんな感じになる。 速度を求めるときなんだけど、今回はrが一定じゃない場合にした。 こっちの方が一般的だからな。 さて、計算してみると、 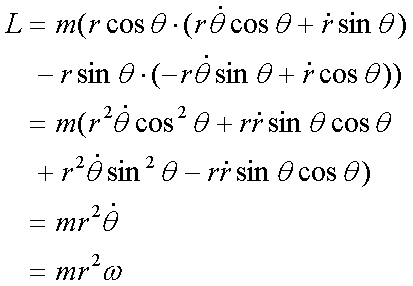 長い式だけど、特に難しくはないよな。 サイン2乗とコサイン2乗の和は1。後ろの部分は同じものだから引いて0。 角運動量の大きさは、mr^2ωってことになるわけだ。 でまあ、これが時間に対し保存するわけで…… 2番目の法則を思い出してみる。 面積速度は一定という奴だ。 図で表すと、 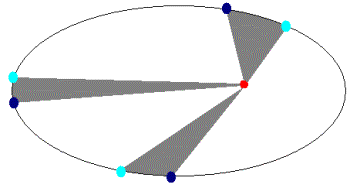 こんな感じ。 色塗ったところのそれぞれが同じ面積ってわけだ。 楕円をぐるぐる回る軌道で、水色から青まで同じ時間が経ってる。だから……遠いほど動きが遅いわけだな。 そりゃ、L一定のとき、rが大きけりゃωは小さい、rが小さけりゃωが大きい。 さて、この面積は実際いくらなのかと言うと、 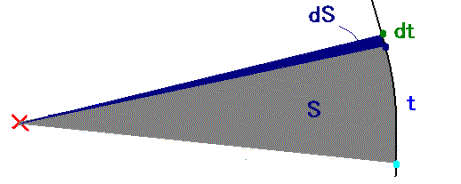 dtだけ経つと、dSだけ増える。  この場合、dtで進んだ距離は、速さのrωにdtをかけたもの。それがそのまま底辺になる。近似してこの三角形なわけだ。 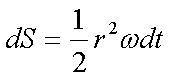 で、三角形の面積がdS。 「ちょっと待って、楕円の軌道だったら底は丸いんじゃない?」 「まあ、そう思うだろうな……でも、微小時間なんだ。微小時間って事は、進んだ距離もちょっと。ということはだ」 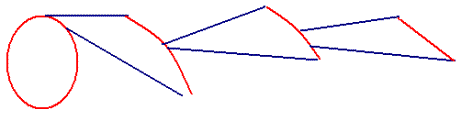 「こんな風に、円の一部の一部の一部の一部……と続ける。最後はもう直線も同然ってわけだ」 で、微小を積み重ねるのは積分の仕事。積分の仕事は面積を求めること。 ってな具合であの面積が求まるわけだな。 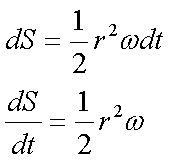 とりあえず面積速度一定ってことが示されればいいから……面積速度って事はもちろん、面積の時間微分な。 でまあ、話を戻す。 角運動量の保存則から、 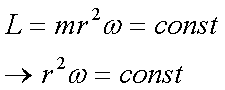 mは質量だから増減なし。定数。定数を定数で割っても定数だから(const/m)も定数。 もちろんdS/dtも一定になるってわけだな。dS/dtが定数なら、同じ時間で積分すればそりゃあ、S一定だよな。 「ちょ、ちょっと待って。ついていけない」 「ああ、待つ待つ」 分からないときは焦らず立ち止まるのが一番だ。 「えっと、まず……角運動量は保存する量なんだよね」 「ああ、その大きさはmr^2ωな」 今のとこは。 「それが一定だから……もともと一定なmを除いた、r^2ωも一定で……微小三角形の面積がちょうどそれに1/2とdtをかけたもの」 「そこまではいいな。そして……面積速度であるdS/dtが一定」 後は積分するだけでSが出るが…… 「うん、てことは……あ、わかってきた」 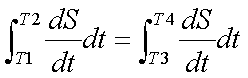 「T1〜T2とT3〜T4が同じ時間だったら、イコールになるってこと?」 「そういうことだな」 だから、改めて法則をもってくると、 惑星と太陽を結ぶ線が一定時間に通過する面積は一定 この式でのT1〜T2(T3〜T4)が、法則で言う「一定時間」ってやつだな。 このケプラーの観測は、角運動量保存を観測した事に他ならないわけだ。 「うん……うん、大丈夫」 そらよかった。 「惑星の運動って、なんだかスケール大きい話だね」 はふーとため息。 そりゃあまあ、考えうる限り一番大きいスケールの物理だわな。 「まあな。スケールでかい運動を支配してるのは重力な」 「ふーん、小さいのは?」 「電磁気力。もっと小さく……原子核レベルになると強い力と弱い力」 「なにそれ?」 首をかしげる稲穂。そういう名前だから仕方ない…… 「専門じゃないからよく分からん。大体説明すると」 強い力:陽子・中性子間に働く力 弱い力:β崩壊時に働く力 「へー……」 「ま、おまけ程度で覚えとけ。ちなみに自然界はこの4つの力で成り立っている」 「うん……で、陽子とか中性子ってなに? あとβ崩壊って?」 はあ、つまり何にもわかってないと。 「……ま、おいおいな」 「うんっ」 「はあー」 ため息と共にノートを閉じる。 稲穂の勉強終了時お決まりパターンだ。 「疲れたか」 「うん。でも、勉強した数学がばしばし使えるのって楽しいね」 「そうだな。数学あっての物理、物理で使っての数学だな」 積分やら外積やら……ああ、そういう意味では行列も複素数もさっさと教えた方がいいな。 「あとは実生活で実感できればいいんだけどなあ」 「?」 なに言ってるんだ? 「ほら、位置ベクトルも速度も実感できるベクトルでしょ? でも角運動量って……外積だし、実際に感じることってないもん」 こいつは……物理嫌いの高校生みたいなこと言いやがって。 「……」 「あ、あれ、ちょっと怒っちゃった……?」 「稲穂、ちょっと来い」 「う、うん……」 今度は俺がひとつため息をつき、稲穂を外へ連れ出した。 達哉に連れられてきたのは……校門にほど近い駐輪場。 そこにあるのは、当然…… 「……自転車?」 首を傾げる私に、達哉がくるりと振り返った。 「稲穂、お前もう自転車に乗れるんだよな」 「うん……」 達哉とゆかりちゃんに押してもらって、練習して、繰り返して……やっと乗れた自転車。 「じゃあ、自転車はどんなときにバランスを崩しやすい?」 「え?」 バランスを崩すって……ぐらつくってことだよね。 「……安定して動いてるのはどんなときだ?」 安定…… 「速いときは……安定してる」 「そうだな」 達哉がうなずいた。 うん、そうだよね。速いと安定。うん。 「じゃあ、速いときと遅いときは、どう違う?」 「どうって……一生懸命こいでる」 「こいだらどうして速くなるんだ?」 え? えっと…… 頭フル回転で走っているところを想像してみる。 「どうしてってそりゃ、車輪が……あ」 ……フル回転? 「そうだ。車輪だな。車輪が回る。回転運動だ。すなわち……」 あ……そっか。 「角運動量……」 「そうだな」 私の言葉に、達哉は小さくうなずいた。 「車輪が勢いよく回る……つまり、角運動量が大きい。ここからは稲穂……自分で考えるんだ」 えっ……? 「宿題」 「え、た、達哉?」 「調べるのもいいけど……できるだけ自分の頭で考えてみろ」 そ、そんな! いきなりそんな事いわれても…… 「安定と角運動量……って、ちょっと抽象的だが、納得できそうな答えが出たら、言ってみてくれ。期限はそうだな……来週沼崎に戻るし、それまでかな」 そこまで言うと、達哉はいたずらっぽく笑った。 「次元に気をつけてな」 私にとっての初めての宿題…… それはちょっと、きつそうだった。 戻る |