Fox ＆ Mathematics 　　　　　〜べんきょう、しよう〜 　　複素数のお話 「角……運動量。うーん」 指をくるくる回しながら、イメージしてみる。 壁の時計を正面から見ると、針の角運動量は壁側に向く。こっちにベクトルが飛んでこないから安心ね。 あ、もしかして時計の針がこっち回りなのはそういう理由なのかも。 「……」 脱線。 「結局、名前しか似てないのよね……」 ごろんと寝返り。 誰もいないお社の中。誰もいないわけじゃないけど、とりあえず私だけ。 うーん…… 「しかも角運動量定義するときに運動量使ってるし」 ｒとｐの外積。順番大事。 「うーん……」 似てるといえば…… 「あ、あと２つともベクトルかあ」 運動量もベクトル、角運動量もベクトル。 「えっと、運動量が大きいものは……」 うん、そうイメージしてみよう。運動量が大きいと…… 「速くて重い。止めるのは結構大変」 そういえば保存するんだっけ。運動量って。 物体はその運動量を保とうとするから止めるのが大変っと。 「角運動量だったらどうかな。定義式からいくと……速くて重くて、距離が大きい？　回ってるんだよね……」 距離はあるけど、それって距離が縮むと速度が速くなって……ってことだよね。 結局車輪だったら…… 「車輪……あ、もしかしたらそのまま回り続ける？」 そかそか、保存するもんね。 変形するわけじゃないから距離一定は当たり前。 ってことは速さを保つから、運動量を保とうとするのと同じなんだ。 保存保存。運動量も角運動量も保存。 ってことは、やっぱりベクトルを変えるのは大変なわけよね…… 「うん、なんとなくわかってきた」 それじゃあ速く回せば勝手に回ってくれるんじゃない？　車輪が。それはつまり角運動量のベクトルが大きいってことだから……そのベクトルの向きを変えるのは大変ってことで、安定。 多分自転車がひゅーっと進んでる運動量も保存してるんだよね。 そう思ったら自転車ってなかなか奥が深いね。 「……と思ったんだけど」 思ったまま、電車の中で達哉に話してみる。 「まあ、正解じゃないか？」 草神駅に着くと、いもスティックをぽりぽり食べながら、達哉がうなずいた。 え、それだけ？ 「食うか？」 「うん」 バスを待つ間、二人でいもスティックをぽりぽり食べた。 もうちょっと褒めてくれても…… 「ねえねえ、角運動量って、どうして必要なのかな」 思い切って聞いてみた。私にはあんまり必要性が感じられないんだけど。 「どうしてって……回転を表すのに便利だからじゃないか」 「にしたって、ベクトルが上向いてるとか使いにくいよ」 いきなり変な方を向かれても困る。 「まあ、気持ちは分かるが……現実は３次元だし、そのうちの２つの次元は位置と方向表すのに使ってるからなあ……あとはその２つの直角の成分しか残ってない」 そう言われればそうだけど…… 「回転方向が２つある限り、それを区別しなきゃ行けないしな……」 「あ、そうか……」 それで正と負を一応定義しないといけないんだ…… 「うーん……」 「ま、そのうち慣れるさ」 笑う達哉。 慣れ……るのかなあ。 でもきっと、大切なのは第一印象だけで逃げないことよね。ずっと向き合ってればそのうち分かる日は来るかもしれないけど、背中向けたらそれまでだし。 「うーん……」 もう少し悩んでみよう。 きっと自分の物にできた時、すごい嬉しいだろうから。 ぐるっと部屋を見回す俺。 「今日は複素数だ」 「複素……数ってことは、数学？」 「ああ、数学だ」 数学も後少しだな…… 「iのやつですよね」 「うん。iのやつ」 志津子ちゃんはもう知ってるようだ。 「習った？」 「えっと、一応は」 そうか……じゃあまあ、序盤は稲穂をビシバシだな。 「まず稲穂、３の２乗はいくらだ？」 「え、９でしょ？」 正解。 「だな。じゃあ‐１００の２乗は」 「１００００。決まってるじゃない」 おっと、ちょっと怒りだしたぞ。バカにされてると思ってるな。 「じゃあ、逆を聞くが、２乗して‐１になる数はあるか？」 唐突な質問に、きょとんとする稲穂。 「え、マイナス？　ならないと思うけど……」 そう言って稲穂ノートにぐりぐりグラフを描く。 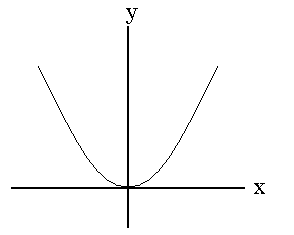うん、見事な二次関数。 「だってこうでしょ？　マイナスになるわけないじゃない」 「まあな。でもそれは実数の領域だけなんだ」 「実数？」 「ま、現実にある数ってとこか」 　うんうんと志津子ちゃんがうなずいた。 「で、もうちょっと数について拡大してみる」 実質最後の拡大だな。 「こういう数を仮定するんだ」 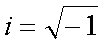「i？」 首を傾げる稲穂。 「そう。i。２乗するとマイナスになるイカレた奴だ」 その一言で全部表したことになるな…… 「とりあえず、上に書いた性質以上でもないし以下でもない。これだけ覚えれば、この数の全てを理解したことになる。こいつの名前を虚数という」 「……なんだかなあ」 「納得できないか」 まあ、気持ちは分かるが…… 「だって実在しないもん。そんなの覚えても仕方ないよ」 「そうでもないんだこれが……」 実在しない関数やらもあるけど使っちまうし、実在しない数を置いて使うのも別に構わないだろう。物理はそんな学問だ。懐が広いあたり日本的だよな……便利なものは使っとかないと。 「覚えても仕方ないってことはない。なかなか使える奴だし」 「そうなの？」 「まあそれはおいおいというか、物理はこれがないとやっていけないぐらい重要」 「ふーん……」 まだ納得してないみたいだったがとりあえずはこれでいいだろう。 「でもさ、コレがあるんだったら、さっき書いたグラフがうそにならない？」 「嘘？　なんで？」 「だってｘの２乗なのにマイナスになるんでしょ？」 あー、そういうことか。 「だから実数の領域だけだって。虚数はな、こんなグラフで表せるんだ」 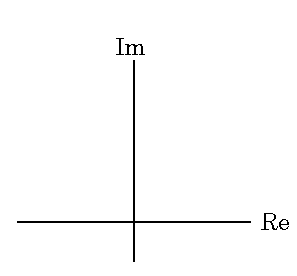軸が違うってわけだ。 「……ReとIm？　ｘがReになってｙがImになっただけ？」 「まあ、そうだ。コレを複素平面と呼ぶ」 「あ、これは初めて見ました」 と、志津子ちゃん。そうなのか…… 「まだ授業ではあまり突っ込んだところまでしてないので……」 そうなのか……複素平面使わず複素数するなんて、なんて面白みのない…… 「で、まあこれは結構面白い性質をもっている」 「例えば？」 「まあ、最たる例が２乗したときなんだが……まずは定義からいこうか」 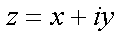「結局ｘｙじゃない」 「細かいことは気にするな。勝手知ったるｘｙ平面と同じに見れた方が分かりやすいだろ？」 「そりゃあ、まあ……」 我ながら無茶だがまあいいや。 「複素数は普通こう表される。特にｘを実部ｙを虚部と呼ぶ。んで、これをグラフ上で表すと」 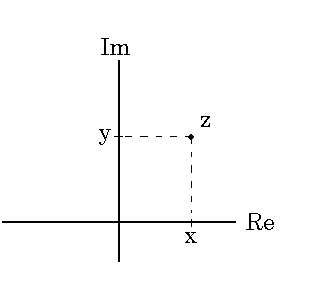「ここになる」 「点？」 まあ、点だわな。 「点。ま、分りやすいだろ？」 「うん、まあ」 じゃ、続き。 「それで、原点からの距離を絶対値と呼ぶ。求め方はまた簡単」 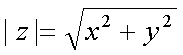「ああ、三角形の」 「そういうこと」 で、まあ、三角の場合も、 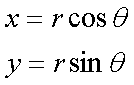こんな感じで置けたわな。 それと同じようにｚの絶対値をｒで表しながら上の式で表すことができる。 「三角のときとかなり似てるね」 「まあな」 というか、ほとんど一緒な。 でだ。これを用いると、ｚは次のように表せる。 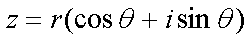「ふんふん。今のをｒでまとめたんだよね。あとiがある。大丈夫」 とりあえずは大丈夫そうだな。 次に、虚部の符号が逆の複素数があるとする。 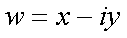これな。 これは、ｚの共役複素数と呼ばれる。だいたい上に線引いて表すな。 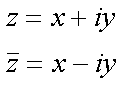グラフで表すと、 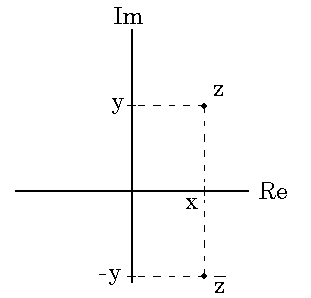こうなる。 複素数の絶対値ってのは、これを使って次の式で求められる。 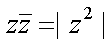「ベクトルと同じ……じゃないんだね」 「ああ、同じじゃない。共役のを掛けて絶対値を求めるんだ」 なんでわざわざ共役のを使うかというと、まあ計算すれば分かる。 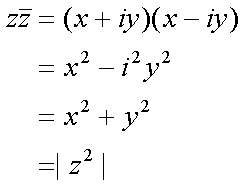上手く行きましたっと。 まあ、こんなもんでいいか。 じゃあ、実際に触ってみるぞ。複素数の掛け算をしてみる。 まず、この二つ 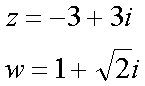とりあえずグラフに表してみろ。 「えっと……」 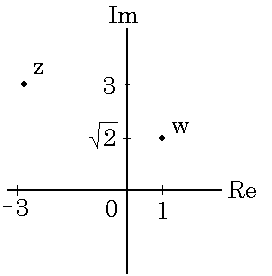「こう？」 だな。じゃあ掛け算。 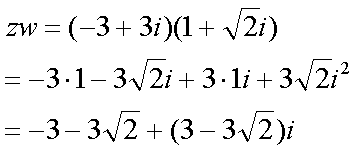うん、まあそうだな。 じゃあ志津子ちゃん、これはどこの点になる？ 「あ、はい。えっと、３×ルート２は……３×１.４ぐらいだから、４．２として……」 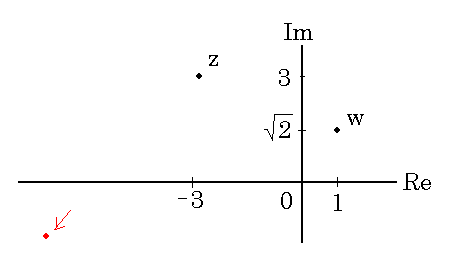「ここらへんですか？」 ん、おっけ。 さて、ここまで露骨に結果が出ると、何が言いたいのか感づくかもしれないが…… さっきの角度で表す式で見るとだ。 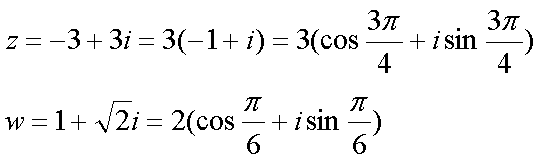ま、こうなる。 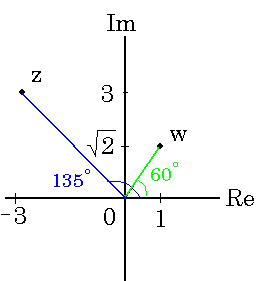んで、掛け算の結果を見るとだ。 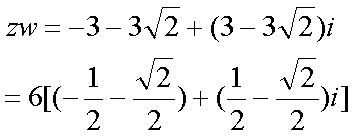でまあ、このかっこの中の数。これは、 「うん、わかるよ」 「マジか」 だってグラフで表すとこうでしょ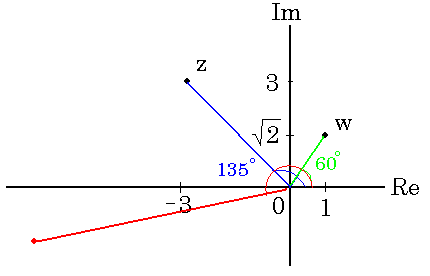？ 「角度足してない？」 こともなげに言う稲穂。 「あ……ほんとだ」 うなずく志津子ちゃん。 「まあ、その通りだけどな」 んじゃ、過程を追うことにする。 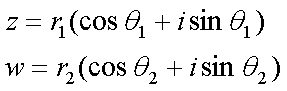まずはこの2つを仮定する。極形式だけどまあ、わかるよな。これで2つの点を表してる。 で、かける。 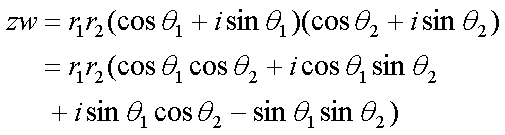整理すると、 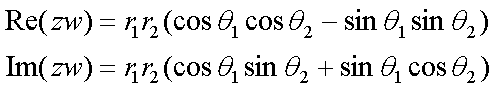これはそれぞれ、ｚｗの実部と虚部がどうだということを表してるわけだ。虚部のＩｍの数にiをつけて、くつけりゃｚｗになる。 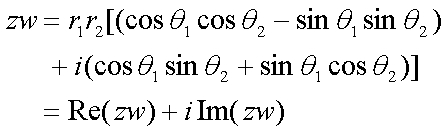さて、さっきのRe(zw)とIm(zw)を処理しようか。 覚えてるかどうかは知らないが、これがある。 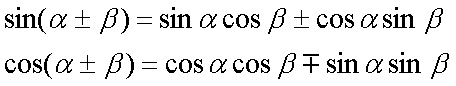「え、これって一発じゃないの？」 「まあ、一発だな。」 「じゃあ、志津子ちゃん、まとめてみて」 「え、あ、はい」 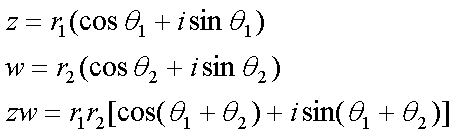「こうですか？」 「はい、正解」 こういう式があるわけだ。 複素数の大きな特徴なんだが、掛け算すると点が回転する。 「回転……」 「えっと、ｚにｗをかけると、絶対値の掛け算の後で、ｗの分だけ角度が増える……ということでよね？」 「うん。そう。だからわざわざ計算しなくてもそれぞれ極形式……絶対値と角度で表すと、掛け算がこんなに単純になる」 この回転が一番分かりやすいのが-１とiだけど…… 「試しにiでやってみな」 と稲穂にいってみる。 「うん、えっと……」 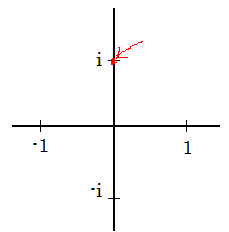「iはここで、掛けると……確か−１」 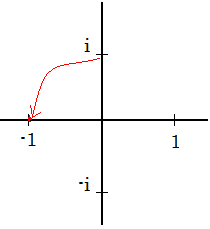「それにまた掛けると−iで、また掛けるとマイナスのマイナス……1に戻る」 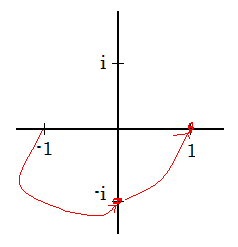「この次はまたiだから……ほんとだ。ぐるぐる回ってる」 「まあ、iの場合は絶対値が1だからそのままだが、1以外の場合は絶対値も変わる事を付け加えておく」 あ、もうあんまり時間ないな。 「じゃあ、今日はこの辺。次は複素数で応用っぽく行こう」 パタンと閉じられる各自のノート。 「複素数って、ベクトルと同じなんですよね」 あ、和と差忘れてた。ま、志津子ちゃんのいう通りベクトルと一緒だからいいか。 「まあ、そうだね。あとはぐるぐる回るのが厄介かな」 厄介というか、醍醐味というか。 「あーあ、次で終わりなんて、残念だなあ」 ぐっと伸びをする志津子ちゃん。 「え、次で終わりなの？」 きょとんとする稲穂。 「ああ、もうすぐ夏休み終わるしな」 「あ、そっか。沼崎に戻るんだ」 そういうことだ。 帰りの電車。 「じゃあまたね」 「ああ、気をつけて帰れよ」 「うん」 志乃上で稲穂を降ろすと、瀬良までと３駅。 今日は早く寝るか……なんて思っていると、ぽんぽんと肩を叩かれた。 「みゃーこじゃないか」 「う……よりりん」 よりりんこと雲浦先生だった。 「よりりんゆーなと言うに」 笑いながら腹をどついてくる。地味に痛い。 「……じゃあ今の生徒にはなんて呼ばれてるんですか」 「……『よりりん』」 「ぷっ」 やっぱり。この人絶対古今東西よりりんとしか呼べないし。クラスのうち誰かしらは呼び名を知っているだろうから、延々とこの呼び方は続いていくわけだ。 「笑うんじゃない。どうしたんだ今日は……って、大学はまだ休みか」 始まるまであと２週間。面倒な授業登録もある。 「ええ、まだ」 「やれやれ、結構なご身分だね……」 肩をすくめるよりりん。高校はもう夏休み明けてるからなあ。ちょっと前から通常の仕事なんだろう。 「それはそうと、文化祭には来るのかい？」 「文化祭……いつですか？」 行けるものなら行きたいけど。 「確か……２５だかそのあたりだった気がする」 「気がするって、それでいいんですか」 教師だろうに。 「まあいいじゃないのさ。多分合っているよ」 まあ、例年からいって多分合っているんだろうけど。 でもその日程じゃ無理だな……もう授業が始まってる。 「で、来るかい？」 「いえ……そのときはもう沼崎ですね」 「おやおや、残念だな。今年のは自信作なのにな」 自信作ねえ……まあ、立派は立派なんだけど。数学教師がやることでもないだろうに。あれは。 「どうせまた数学準備室に飾ってるんでしょ？」 また寄った時に見せてもらえばいいし。 「ああ、もう１０体目……バザーにでも出そうかと考えてるよ」 ついに大台か。他の数学の先生方はどう思っているんだろう。あんなもの並べられても…… 「校長室にでも寄贈すればいいじゃないですか」 「冗談。そんな勿体無いことできるわけがないでしょ」 「隠しマイクとか仕込んで」 「さて、なんて言って渡そう……」 この人は…… 「冗談だよ。そんな顔をしない。相変わらずだね、みゃーこは」 とまあ、こんな会話をしているうちに我が瀬良へとたどり着く。 よりりんはもうちょっと先らしい。 「じゃあ、またな」 「はい、また」 よりりんの乗る電車を見送ると、駅を出て家へと向かった。 『また』か。卒業生ってそう母校に行くもんでもないと思うが…… ま、悪い気はしない良い挨拶だしな。『また』って。 戻る