複素数のお話２

Fox ＆ Mathematics
　　　　　～べんきょう、しよう～

　　複素数のお話２

「あっつい！」
「暑いな」
草神でバスを待つ。
これがまた意外と乗り継ぎが悪い。
「またえらく薄着だな」
白のノースリーブがまぶしい本日の稲穂。
「そう？　でも暑いし……」
ぱたぱたと胸元を仰ぐ。
……ちょっと見えそうじゃないか。大変目のやり場に困るんだが。
「それはそうと、お前胸ないのな」
ドスッ
「ぐっ……」
腹に鈍い痛みが走った。
「つまんないこと言わないのっ」
気にしてたのか、やっぱり……
そうこうしているうちにバスが来た。
うう、腹が痛い。

そんなこんなで佐倉邸。
そして今日は複素数の続き。
「え、続き？」
「ひと段落したんじゃあ」
不服そうな二人。なんでだ。
「まあまあ。そうあっさり終わっても面白くないでしょ？」
「うーん……」

前回は掛け算をやったわけだけど、今回は割り算について考えてみる。
取り出だしたるこいつ。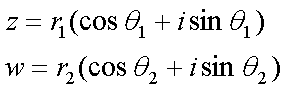

さて、割ろうか。

「え、私？」
きょとんとする稲穂。
「できるとこまででいいからやってみろ」
「うん……」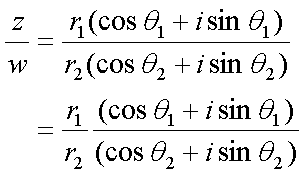

「うんー……？」
いきなり止まるか。
「分母に共役を掛けてみろ。勿論つじつま合わせるために分子にも同じものを掛けるんだぞ」
「共役って……なんだっけ。iのとこが正負逆なんだっけ？
「そうそう」
うなずいたのは志津子ちゃん。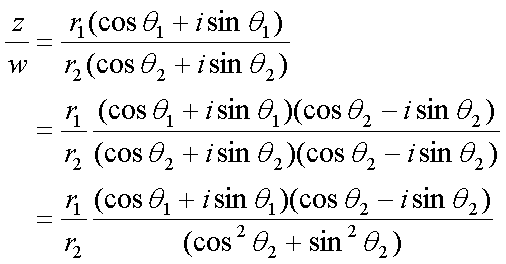

「こう？」
分母分子に共役な1を掛けて……その後も大丈夫だな。よしよし。
「あれ？　分母消えそう」
「消えるな」
消えてもらわないとちょっと困る。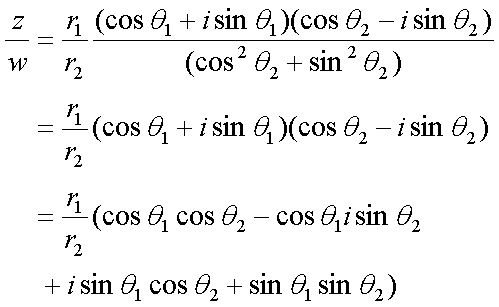

「あれー？　これってつまり、」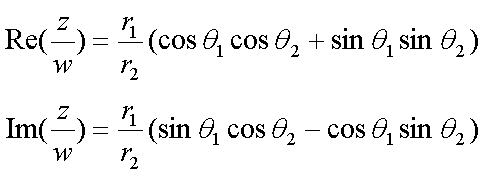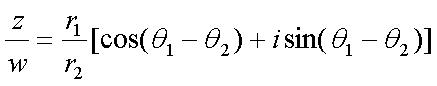

「ってこと？」
「正解」
なんとかなったな。うん。
というわけで、前回の掛け算の結果。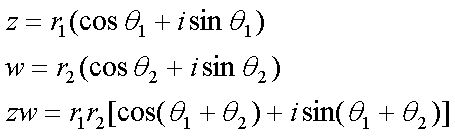

に対して、次のこれが得られる。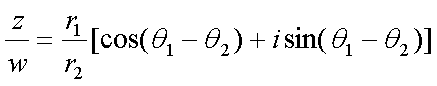

「引き算なんだね……」
「そうなるな。あと絶対値は割り算。覚えやすいことこの上ないな」
結局かけても割ってもぐるぐる回る。回る方向が逆なだけだな。

さて、ここでちょっと話を変える。
複素数のｎ乗について考える。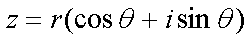

これな。これをだ、ｎ乗すると、さてどうなる？
「ｎ乗ということは……ｎ倍角度が大きくなりますよね。あと絶対値がｎ乗されます」
その通り。
志津子ちゃんなかなかやるね。
結果を表すと、こうなる。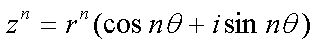

これの、特に絶対値が１のときを考える。つまりｒが１だから……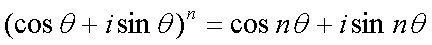

この式のことをだ、ド・モアブルの定理と呼ぶ。
まあ、なんてことはない。物理やる上ではそんなに重要でもないけど、一応覚えておこうな。

ほんじゃあまあ、ちょっと練習。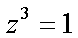

これ解いてみようか。
「え……」
意味分かってない稲穂。
「これって、答えは１じゃないんですか？」
その通り。
「１もあるね。でも基本的に、ｎ次関数の解はｎ個あるはずだから……この場合は解が3つあるはずだよね」
「えー……？」
「あと２つ……」
短い式を見ながら考え込む二人。
仕方ない。
「ここで取り出すのが、複素平面」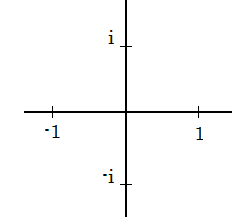

「うん。それで？」
「考えろよ」
ド・モアブル出したんだしなんとか分かりそうなもんだが。
「うん……」
再びじっと見入る二人。
やがて、
「3乗して、１……あ！」
志津子ちゃんが思いついたようだ。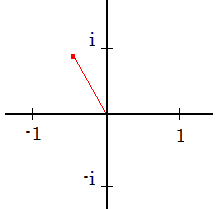

「ここですか？」
「つまり？」
「えっと……３倍したら２πになる角度だから……」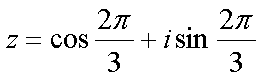

「これですか？」
「正解」
良くできました。
さて、稲穂。
「あとひとつは？」
「えー……？」
「ヒント、２回転」
まんまじゃないか、俺。
「２回……あ」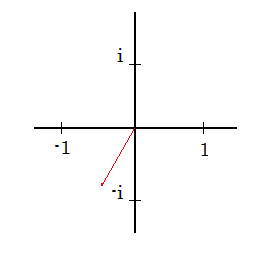

「ここだね？　３倍したらぐるぐる回って１に行きそう」
「正解」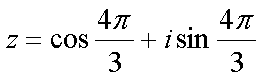

「こういうことだな。結局ｎ倍した角度が２πの整数倍になればいいわけだ」
「へえ、これが1の三乗根……繋いだらきっと正三角形だね」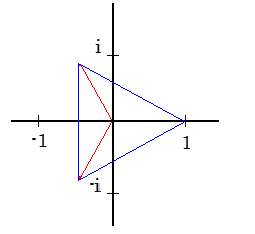

「ほら」
「そうだな。ついでに四乗根もやってみるか？」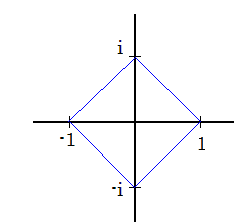

「ま、そうだわな」
「五乗根は……72°ずつかな？」
む、なんか稲穂がうきうきしてきてるぞ。
「うん、じゃあ……」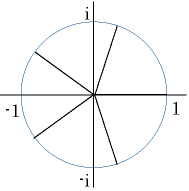

「あ、正五角形になりそう」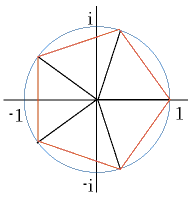

絶好調の稲穂。
「達哉、達哉」
「なんだ？」
「面白い」
子供のように笑う。
正五角形ひとつで幸せになれるとは安い奴め。
「良かったな」

しばらくして……
「じゃん、できあがり！」
「ほう」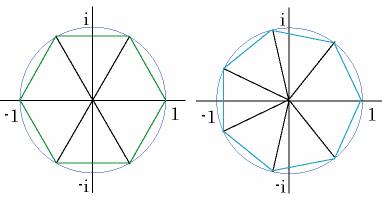

六角形と七角形か。
「へえ、なかなかいい出来じゃないか」
「でしょー」
楽しそうな稲穂。
まあ、勉強は楽しまないとな。

さて、話は変わってと。ちょっと思い出してみようか。
「思い出す？」
ああ、思い出す。
複素数の計算でだな……絶対値はこの際置いといて、
ド・モアブルの式をもってくる。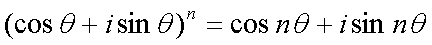

これな。
「うん……？」
ｎ乗するという作業の結果、角度はｎ倍になる。
というか、複素数では掛けた物は角度を足したものになる。
割った物は角度を引いたものになる。
「だね」
「そうですね……」
つまり、掛けると足して、割ると引くもの。
さて、似たようなのなかったか思い出してみるか。
「うー？」
「うーん……？」
分からないか……まあ、そうかもな。
はい、ここにxのa乗という数がありまーす。
「あ」
志津子ちゃんは気がついたかな……
「うん？」
じゃあ、このxのa乗に……xのb乗を、さてどうしようか、稲穂。

「わ、私？」
「ああー……」
志津子ちゃんはどうやら分かった様子。
「ちょっとまってね……うーん……aとb？　うーん……？」
じっとにらめっこの稲穂。
今の会話のテーマからすりゃ、分かってもいいような、もんだけどな。
「あ、あー！　あー……」
驚いて喜んで落ち込む稲穂。何やってんだ一体……
「いちいち激しい奴だな」
「気付いて、理解して、気付けなかった自分にがっくりきたの」
「なるほど。じゃあ張り切ってどうぞ」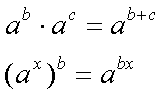

「この何乗って言う部分！　こういうことが言いたいのよね」
「その通り」
掛けたら足すことになり、何乗かすれば何倍になり。
複素数の角度と指数は何となく似ているような気がするよな。

でだ。
ちょっとそれっぽく関係式に乗せてみようじゃないか。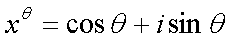

二乗してみると、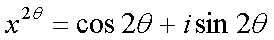

ほら、一緒だよな？

「そうだけど……なんか騙されてる気がする」
「私も……」

OKOK。まあ騙してるんだけどさ。
どうでもいいが、上のはあっさりと崩壊する。
θで微分してみると、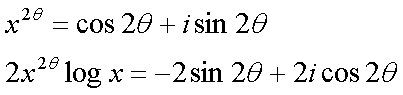

はい、もう意味わかんないね。
２で割っても、ログが存在してる。気持ち悪いね。
「あ、でも、ログが無かったらいい線行くよね」
「うんうん……というより、ログが無かったら成り立ってるんじゃ……」
やってみるか？
じゃあ、ログを消すにはどうしたらいい？
「e……」
ぼそっと稲穂。
「正解」
「e？」
「あ、志津子ちゃんやってなかった？　自然対数」
「少しやったような……いえ、大丈夫です」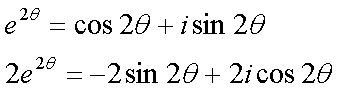

「あ、でもまだずれてるんだ……Iを掛けたらいけるんじゃない？」
「iっつーか、-iが右辺に掛かればいいよね」
「右辺に-iですか？」
あんまり分かってない様子の志津子ちゃん。
「そもそも、微分した上でこの形が出てきてるわけだから……」
「あ、じゃあ」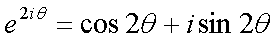

「これでいいんじゃない？」
勘が良すぎるぞ、稲穂。
「よし、じゃあ微分して計算してみろ」
「うん」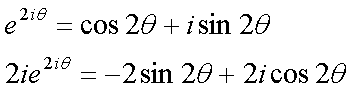

「ええっと、両辺を2iで割ればいいのよね」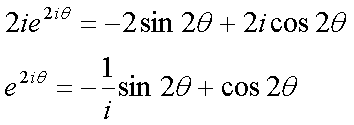

よし、当然のように、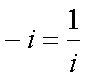

だから……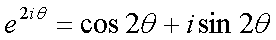

だな。見事に微分しても成立したってわけだ。とりあえず2を取り除いて……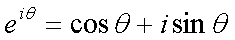

これが一番シンプルな関係式だな。。
次は3乗してから微分しようか。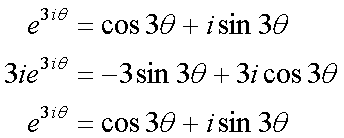

問題ないね。絶好調。
「へえ、それじゃあ指数と三角が虚数で結びついたというわけですか」
「そういうこと」
ああ、めでたいめでたい。

「この関係式を、オイラーの公式という」
「これ……実はすごくない？」
目を丸くしている稲穂。
「すごいってば」
「うわ……」
ノートを手に持って感動している様子。
「数学史上まれに見る美しさだよな」
「うわあ……」
まだ感動に打ち震えている様子。
「ああー、あたし、今数学やって良かったって思った」
「そうかそうか」
正直な奴め。
「私も……これはすごいと思います。ここまできれいに成り立つと……うーん」
「まあ、これは完全でもなくて……まあいいか。志津子ちゃん今日で一応最後だし、おまけ程度に聞いて」
「はい」
「稲穂はまじめに聞けな」
「うん」

まあ、最初に置いた時からして問題なんだが、これはθが連動してるだけであって、イコールかどうかは分からない。
「うん、そうだね」
「そうですね」
普通、これを求めるときは、展開っていう作業を経るんだ。
で、これから展開の話をしようか。大学の数学だから、志津子ちゃんはあまり力入れて聞かなくていいよ。
稲穂はちゃんと聞いておけな。
「はい」
「うん」
二人の声が重なって聞こえた。

戻る