| 高設定である確率 hp |
|---|
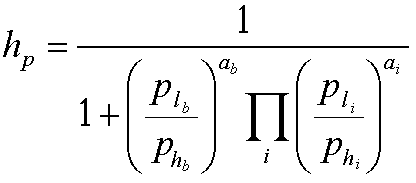 |
低確率時がpl,高確率時がphである小役が,設定判別ゲームで出現した場合,高確率時である可能性hpは
hp = ph / ( ph + pl )
である。ただし,高設定台と低設定台の置かれる偏り(設置のされ易さ)は考慮に入れてない。
また,これが2回連続で起きたならば,
hp = ph2 / ( ph2 + pl2 )
となり,更に別の小役(低確率時p'l,高確率時p'h)が出現したならば,
hp = ph2p'h / ( ph2p'h + pl2p'l )
である。そして,外れた(何もフラグの立っていない純粋な外れ)場合も同じく,その確率をplb(低確率時),phb(高確率時)とすると,
hp = phb / ( phb + plb )
である。つまり,小役n種類の確率を,pl1,pl2,・・・,pln(低確率時),ph1,ph2,・・・,phn(高確率時),外れの確率をplb(低確率時),phb(高確率時)とし,小役のフラグがたった回数をa1,a2,・・・,an,外れの回数をabとすると,
| 高設定である確率 hp |
|---|
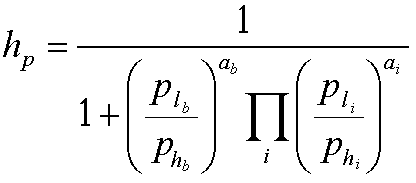 |
となる。この式は前述した式のようにphが2回出てこないように,前述の式の分母分子をphで割っています。
| 種類 | 低確率 | 高確率 |
|---|---|---|
| 2枚 | 1601 | 2100 |
| 4枚 | 671 | 1550 |
| 10枚 | 180 | 1508 |
| 15枚 | 132 | 675 |
| Replay | 2245 | 2245 |
| big | 63 | 66 |
| reg | 34 | 37 |
| 外れ | 11458 | 8203 |
さて,実例を出していきましょう。今回は,バーサス(ユニバーサル販売:現アルゼ)を使ってやってみよう(設定4以上判別)。
右の表は,各小役とボーナスの確率である(分母の16384は省略してある)。ビッグとレギュラーは,それぞれ比較する設定のものを仮に選ぶ。本当は設定が分からないため,これらの確率も分からないのだが,外れの確率に影響を及ぼすのでちょっとでも正確になるように入れる。つまり,外れの確率を出すにはすべての小役,リプレイとボーナスの確率を全体から引くしかないからである。また,設定によって違う確率の小役の場合も同様に比較する設定のものを仮に入れる。
判別に使う小役の選定であるが,当然高確率と低確率に差があるものを選ぶ。リプレイのように同じ確率のを入れたとしても約分されて消えてしまう。それと,当然ボーナスは対象外。つまり,2枚,4枚,10枚,15枚役がその対象となる。
よって,2枚,4枚,10枚,15枚の小役の出現回数をそれぞれ,a2,a4,a10,a15,外れの回数をabとすると高設定である確率hpは,
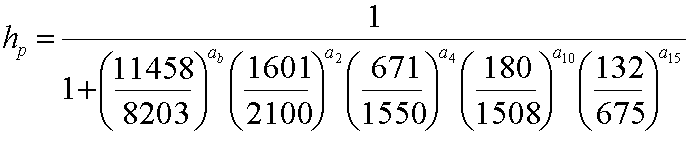 |
となる。そこで,それぞれの出現回数を想定して計算してみよう。
| 種類 | 2枚 | 4枚 | 10枚 | 15枚 | 外れ | 高設定の確率 |
|---|---|---|---|---|---|---|
| 例1 | 2 | 1 | 0 | 0 | 8 | 21.524% |
| 例2 | 0 | 0 | 2 | 0 | 8 | 82.887% |
| 例3 | 2 | 0 | 1 | 1 | 5 | 93.272% |
| 例4 | 4 | 1 | 0 | 0 | 3 | 71.502% |
| 例5 | 0 | 0 | 0 | 0 | 10 | 3.416% |
| 例6 | 0 | 2 | 3 | 0 | 6 | 99.764% |
下の表は10枚役が2回出現したときと,外れ回数による可能性の変化を示す。
| 外れ回数 | 高設定確率 | 外れ回数 | 高設定確率 | |
|---|---|---|---|---|
| 0 | 98.595% | 7 | 87.123% | |
| 1 | 98.049% | 8 | 82.887% | |
| 2 | 97.295% | 9 | 77.617% | |
| 3 | 96.262% | 10 | 71.285% | |
| 4 | 94.855% | 11 | 63.994% | |
| 5 | 92.958% | 12 | 55.994% | |
| 6 | 90.431% | 13 | 47.670% |
出現回数を入力すると高設定確率を計算するJavaScriptを書いたので,利用してください。
前述の応用として,総回転数とビッグ回数の情報から,設定別にその可能性を弾いてみよう。
ここでも,設定別に設置され易さは考慮に入れない。任意に選んだ台が,どの設定が選ばれているかは,同様の可能性とする。
さて,細かい計算過程は省いて,いきなり計算式をあげる。n回プレイされ,ビッグ回数がb回の台が設定jである可能性hj(b,n)は,設定1から6までのビッグ確率をそれぞれq1,q2,q3,q4,q5,q6とすると,
| 設定jである確率 hj(b,n) |
|---|
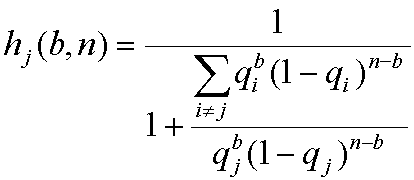 |
となる。実際に計算してみよう。ここでも,バーサス(ユニバーサル販売:現アルゼ)を例にする。
| 4,000プレイで17回ビッグ(1/235.294) | ||
|---|---|---|
| 設定1 | 13.325% | 45.551% |
| 設定2 | 15.329% | |
| 設定3 | 16.896% | |
| 設定4 | 17.917% | 54.449% |
| 設定5 | 18.266% | |
| 設定6 | 18.266% | |
これは,ビッグの引きが設定6よりいくらかよい場合の計算例。この程度では各設定の差も少なく,さらに3以下と4以上の場合の差も少なく設定の判断材料にはならない。なお,バーサスは設定5と6のビッグ確率が同じため,パーセンテージは同じ数値になる。
| 3,520プレイで22回ビッグ(1/160.000) | ||
|---|---|---|
| 設定1 | 5.566% | 28.523% |
| 設定2 | 9.045% | |
| 設定3 | 13.912% | |
| 設定4 | 20.351% | 71.477% |
| 設定5 | 25.563% | |
| 設定6 | 25.563% | |
これは,私がある時拾った台。ここまで凄いとさすがに高設定の可能性は高くなる。しかし,勘違いしやすいのが試行回数(プレイ回数)が多いほど信頼性があがるわけで,同じ1/160の引きでも例えば640プレイで4回ビッグでは3以下の可能性45.604%,4以上の可能性54.396%となってしまう。
| 4,500プレイで8回ビッグ(1/562.500) | ||
|---|---|---|
| 設定1 | 36.279% | 75.732% |
| 設定2 | 23.954% | |
| 設定3 | 15.500% | |
| 設定4 | 9.848% | 24.268% |
| 設定5 | 7.210% | |
| 設定6 | 7.210% | |
逆に今度はハマった場合の計算例。だいたい4,000プレイはこなさないと可能性に開きが出てこない。
| 1,000プレイで0回ビッグ(-) | ||
|---|---|---|
| 設定1 | 24.271% | 61.274% |
| 設定2 | 20.197% | |
| 設定3 | 16.806% | |
| 設定4 | 13.984% | 38.726% |
| 設定5 | 12.371% | |
| 設定6 | 12.371% | |
最後にストレート1,000回ハマリの例。まあ,こんなもんでしょう。当然,設定判別が効く台はそれをやったほうが効果的である。
一般に,設定によって異なる確率の役(ボーナス,小役)がm個あり,それぞれ設定cでの確率をq(c,1),・・・,q(c,m)とし,フラグ成立回数をa1,・・・,am,総回転数をn,外れ回数をnbとすると,
| 設定jである確率(一般版) hj |
|---|
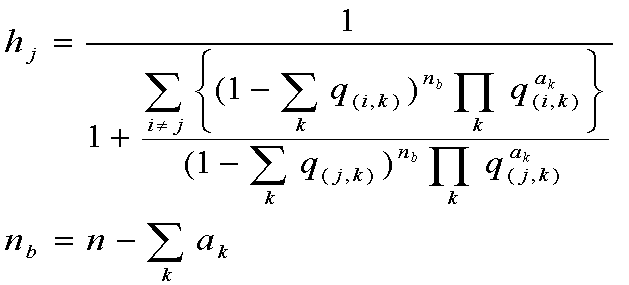 |
となる。目眩がしそうな式だが,これもJavaScriptにしてあります。
結論を言えば,かなり試行しないと可能性に開きが出てこないので,満足な試行を得られるまでに閉店となることでしょう。つまり,ホールのビッグ回数と回転数のメータは,あまり当てにならないということです。
このページに載っていることを運用した結果についての責任は一切負いません。